Idiomatic Python
Table of Contents
Introduction

Scientists are great programmers: they code the fastest and smartest algorithms! But they are also poor programmers: they learn through experiments and often write ‘unprofessional’ code.
Most languages have a preferred way of being used. In this bytes ‘n’ biscuits we will discuss the idiomatic way to write python.
Normally, scientists program like this:
Identify problem.
Keep coding until problem is solved.
What we should add is:
Polish the code just a bit so it is maintainable.
Topics we’ll cover
We’ll use Pycharm to explore
Idiomatic Python
(Bayesian data analysis)
Idiomatic Python
Writing Idiomatic Python by Jeff Knupp is full of simple ready-to-use tips to write idiomatic Python.
Selection of idioms:
1.2.1 Use the enumerate function in loops instead of creating an “index” variable
1.3.1 Avoid using a mutable object as the default value for a function argument
2.3.1 Use a list comprehension to create a transformed version of an existing list
2.8.1 Use a context manager to ensure resources are properly managed
3.5.1 Use the
if __name__ == '__main__'pattern to allow a file to be both imported and run directly
And even more (from Teake):
1.3.5 Learn to treat functions as values
1.1.5 Avoid comparing directly to
True,False, orNone1.2.2 Use the in keyword to iterate over an iterable
2.3.5 Use all to determine if all elements of an iterable are True
2.9.1 Prefer a generator expression to a list comprehension for simple iteration
3.3.3 Do not use
from foo import *to import the contents of a module
Things I learned:
1.2.3 Use else to execute code after a for loop concludes
3.4.2 Use
__main__.pyto run packages as scripts2.3.6 Use the
*operator to represent the “rest” of a list
Problem: UFO detection
We’ll localize an UFO as an example problem.
Setting
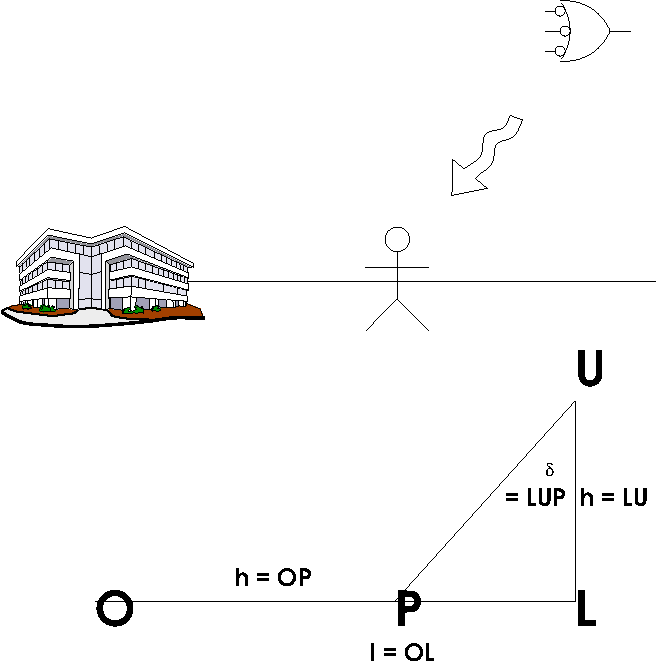
See figure. We’ve just build a telescope (O), and discovered that there is a UFO (U) that is killing many people (P). We need to discover where the UFO is.
The UFO sends out a death ray in random direction delta.
A person dies at distance h.
Given enough measurements of h, what is the location of the UFO, l.
For simplicity we assume that the height of the UFO is known, at say 2. A first simple method to find l might be to average all measurements of h. But it turns out that h follows a Cauchy distribution and its mean does not converge!
We therefore need to do a Bayesian analysis, or at least a maximum likelihood analysis. This example is based on the excelent book Sivia Skilling Data Analysis A Bayesian Tutorial.