Void Hierarchy
Excursion Set Formulation
Excursion Set Formulation
project in collaboration with Ravi Sheth (Univ. Pittsburgh)
highres figures MNR7661
gzipped tar file
Figure 1. The derived void size distribution function:
a peaked distribution centered on a characteristic size, evolving self-similar in time.
A telling and significant contrast to the mass distribution for halos (and galaxies),
with its characteristic divergent power-law trend towards low masses.Figure 2. Void substructure.
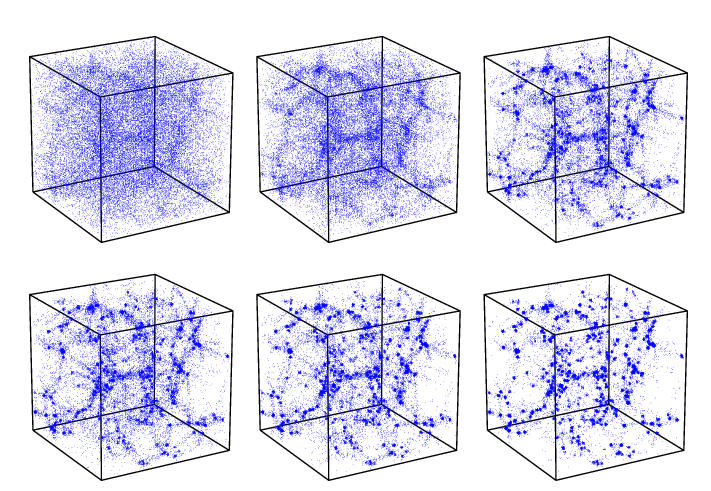
A simulation of evolving SCDM void: 3-D image, sequel of 3 zoom-ins
Reference:
Void Hierarchy: Evolution (project with E. Platen)
We present a model for the distribution of void sizes and its evolution in the context of hierarchical scenarios of gravitational structure formation. We find that at any cosmic epoch the voids have a size distribution which is well-peaked about a characteristic void size which evolves self-similarly in time. This is in distinct contrast to the distribution of virialized halo masses which does not have a small-scale cut-off.
In our model, the fate of voids is ruled by two processes. The first process affects those voids which are embedded in larger underdense regions: the evolution is effectively one in which a larger void is made up by the mergers of smaller voids, and is analogous to how massive clusters form from the mergers of less massive progenitors. The second process is unique to voids, and occurs to voids which happen to be embedded within a larger scale overdensity: these voids get squeezed out of existence as the overdensity collapses around them. It is this second process which produces the cut-off at small scales.
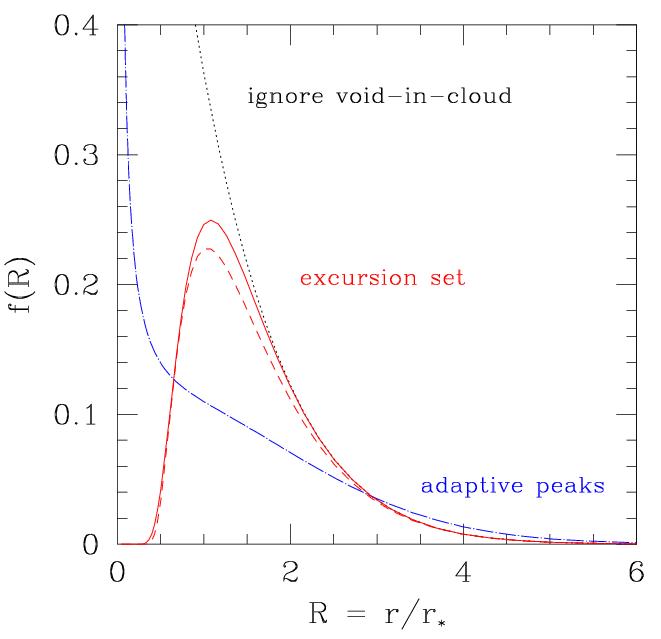
In the excursion set formulation of cluster abundance and evolution, solution of the {\it cloud-in-cloud} problem, i.e., counting as clusters only those objects which are not embedded in larger clusters, requires study of random walks crossing one-barrier . We show that a similar formulation of void evolution requires study of a two-barrier problem: one barrier is required to account for voids-in-voids , and the other for voids-in-clouds . Thus, in our model, the void size distribution is a function of two parameters, one of which reflects the dynamics of void formation, and the other the formation of collapsed objects.
Void Hierarchy manuscript Sheth & van de Weygaert, astroph version:
Manuscript
Mykonos script Sheth & van de Weygaert:
Manuscript
Void Hierarchy Mykonos ppt
presentation:
Presentation
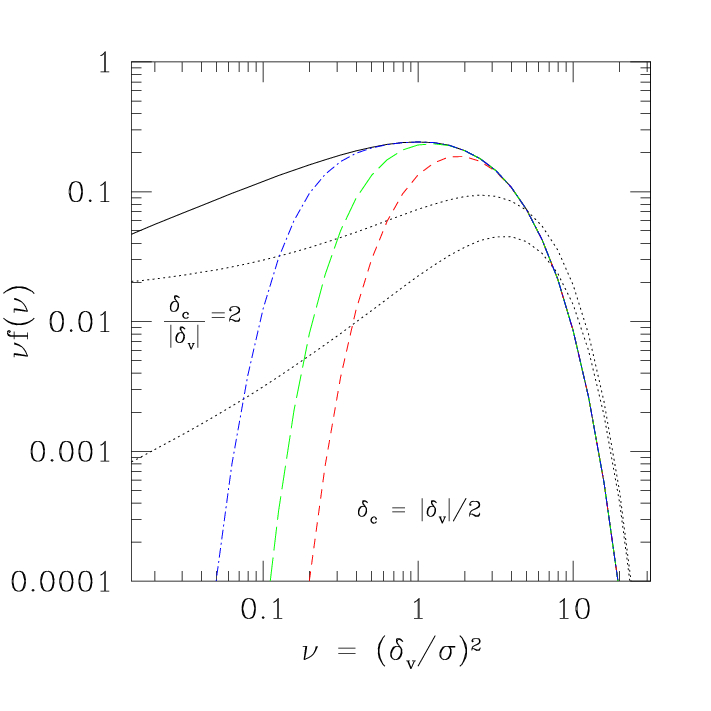
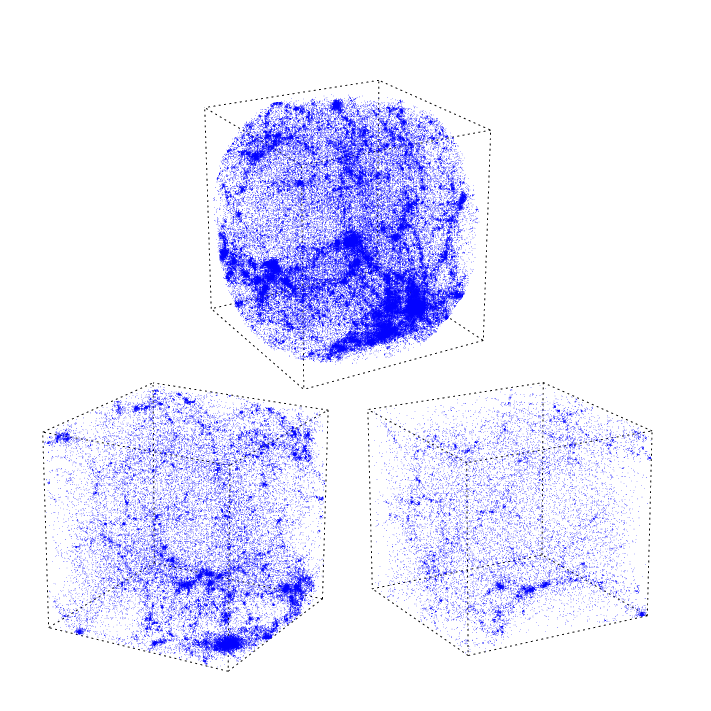
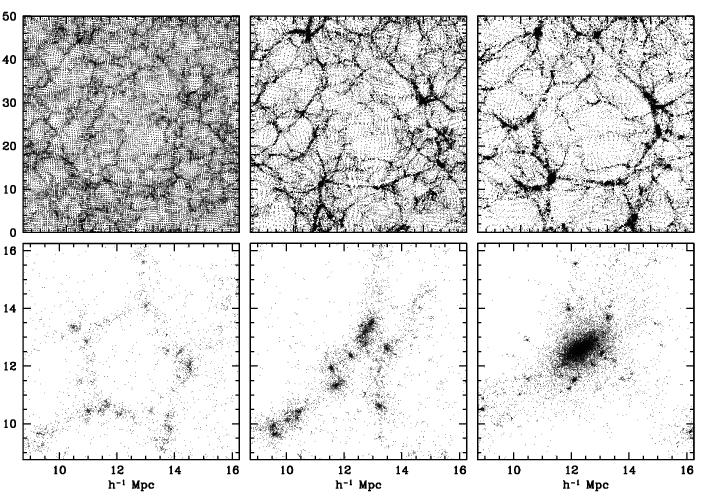
Figure 3. Hierarchical Void Evolution.
Illustration of the two essential ``void hierarchy modes'':
(top) the void-in-void process, with a void growing through the
merging of two or more subvoids; (bottom) the void-in-cloud process:
a void demolished through the gravitational collapse of embedding region.
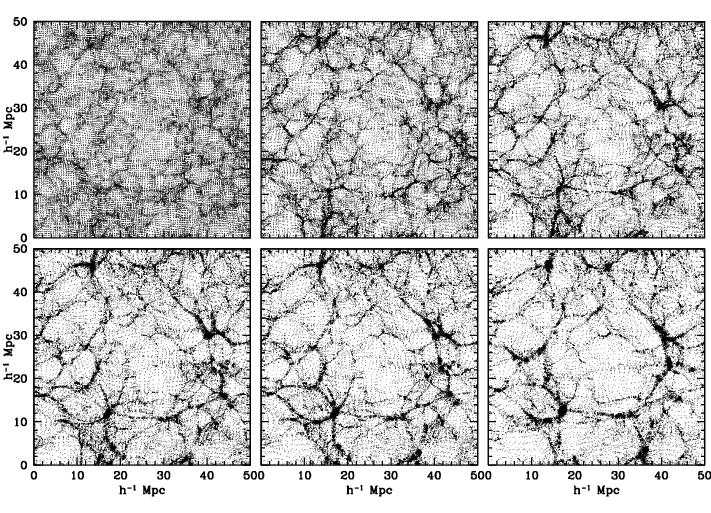
Figure 3a. Hierarchical Void Evolution.
A simulation of the development of a SCDM void:
displaying the void-in-void aspect of the evolving void hierarchy.
Six timesteps, from topleft to bottom right.
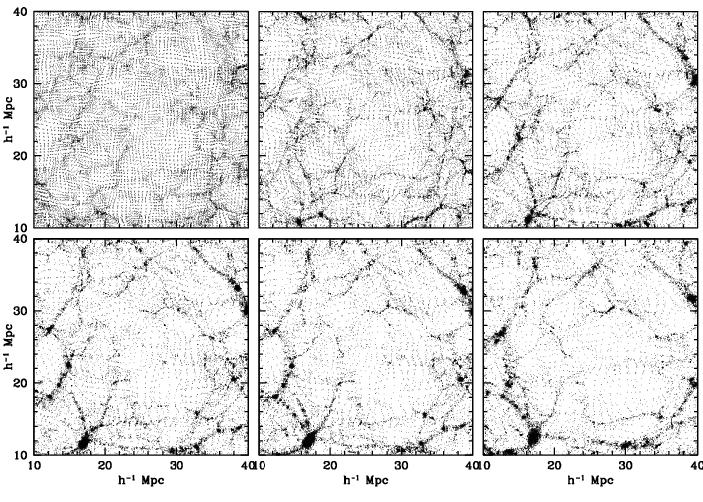
Figure 3b. Hierarchical Void Evolution.
Zoom-in of Fig. 3a
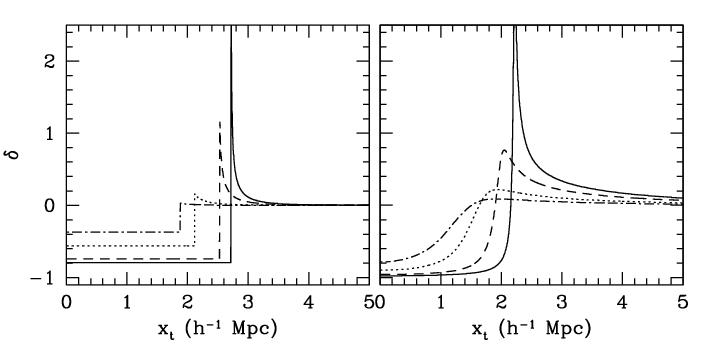
Figure 4. Spherical Model Void Evolution.
Development of a tophat void (left),
and the tendency of a spherically symmetric CDM void to evolve towards a
tophat configuration (right).
Figure 5. Spherical Model Void Evolution.
Comparison evolution of spherically symmetric CDM void:
one with average steepness "x=" (see BBKS) of density profile (left),
the other with a more shallow density profile "x=2":
To develop a tophat profile the initial profile needs to be sufficiently steep !
the other with a more shallow density profile "x=2
To develop a tophat profile the initial profile needs to be sufficiently steep !
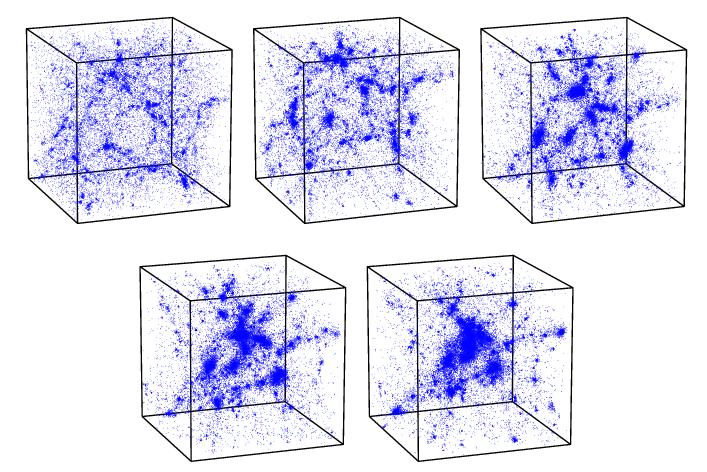
Figure 6. Collapsing Void.
3-D view of collapsing void from N-body simulation.
The void-in-cloud aspect of the void hierarchy.
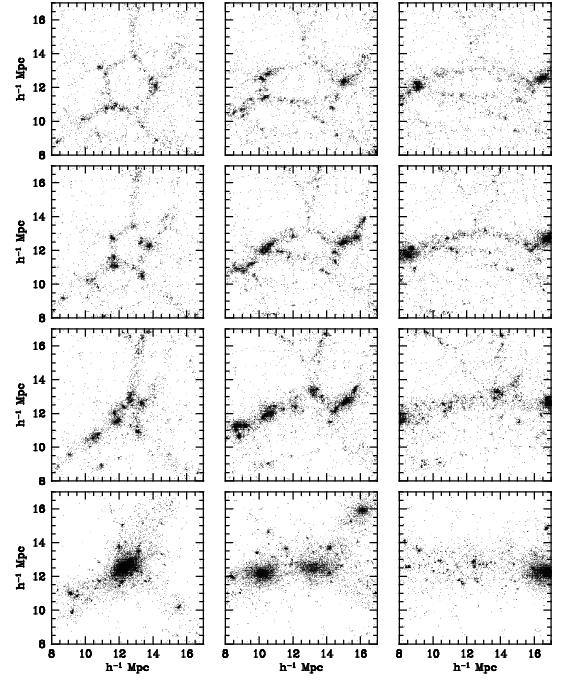
Figure 7. Collapsing Voids.
Three examples from N-body simulations:
the void-in-cloud aspect of the void hierarchy.
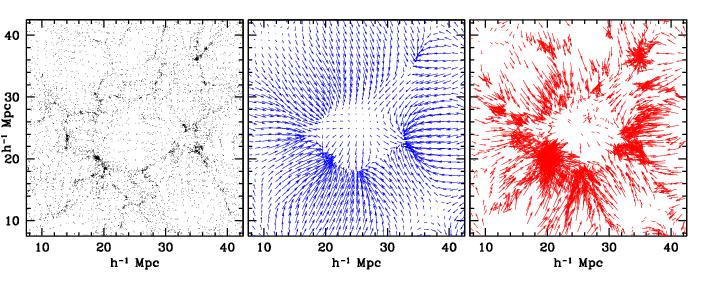
Figure 8. Collapsing Void: Dynamical Context.
Particle distribution (left), gravitational field (centre) and velocity field (righthand)
in and around a collapsing void (from a SCDM N-body simulation).
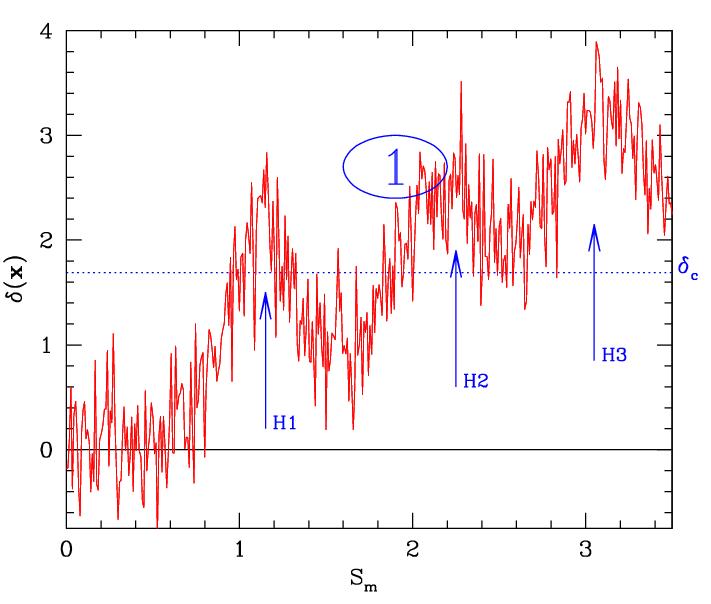
Figure 9a. Excursion set formalism.
Halo Excursions
Figure 9b. Excursion set formalism.
Void Excursions
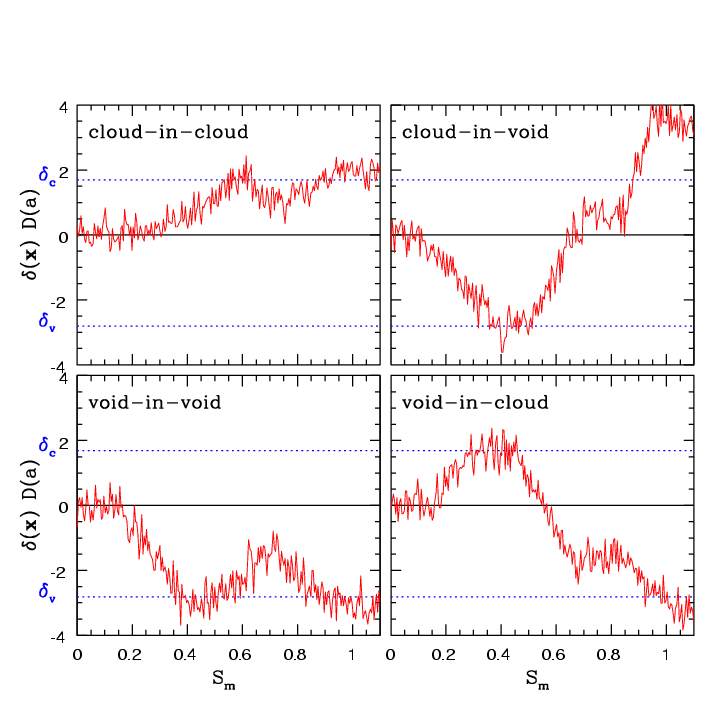
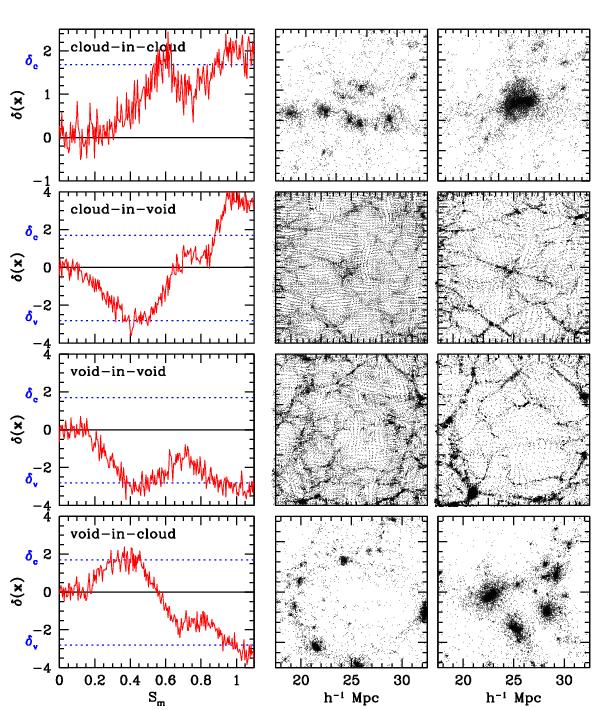
Figure 10. Excursion set formalism.
Four modes of excursion behaviour:
cloud-in-cloud, cloud-in-void, void-in-void and void-in-cloud
Figure 11. Excursion set formalism.
Illustration of physical significance
modes of excursion behaviour:
cloud-in-cloud, cloud-in-void, void-in-void and void-in-cloud
Figure 13a. Kinematic Voronoi model.
Evolution of galaxy distribution in Voronoi foam.
6 consecutive slices, 3-D view.
