Sterstructuur

Sterren kunnen we op een eenvoudige manier beschrijven door middel van drie vergelijkingen: de vergelijking voor hydrostatisch evenwicht, de toestandsvergelijking voor een ideaal gas en de stralings transportvergelijking. We zullen deze vergelijkingen hier niet uitgebreid afleiden. Ze zijn te schrijven als volgt:

1.  Hydrostatische evenwicht:  dP/dr = - G M(r) r (r) / r2

waar P de druk is aan de rand van een bol met dichtheid r en straal r

2.  Toestandsvergelijking:  P(r) = n(r) k T(r) = r(r) k T(r) / (r) mH

waar n de deeltjesdichtheid is, k de konstante van Bolzmann (1.38 x 10-23 J/K), mH de massa van een waterstofatoom (1.67 x 10-27 kg) en  de gemiddelde moleculaire massa van de deeltjes (= de gemiddelde massa per deeltje  uitgedrukt in mH ; b.v. voor een gas bestaande uit alleen neutraal waterstof is  = 1, voor een gas bestaande uit geioniseerd waterstof, dus protonen en electronen is  = 1/2)

3.  Stralingstransport:  L(r) = -64  r2 T3(r) / [3 (r) (r)] dT/dr

waarbij s de constante van Stefan-Bolzmann is (5.67 x 10-8 J/m2 s K4),  de opaciteit (het absorberend vermogen) van het gas, T de temperatuur en L de intensiteit van het stralingsveld. De wet van stralingstransport beschrijft hoeveel straling (energie) er door ieder oppervlaktelementje stroomt in een ster als functie van r, T, k en r.  Voor de straling die uiteindelijk uit het oppervlak van een ster met straal R stroomt geldt natuurlijk dat die evenredig is met het product van het oppervlak en de straling van een zwart lichaam per oppervlakte eenheid (de integraal over de Planck functie die oplevert: I =  T4); m.a.w. L = 4  R2 T4 . Dit is de wet van Stefan-Bolzmann.

Deze wetten beschrijven een ideale ster en we kunnen ze gebruiken om een aantal basis afhankelijkheden af te leiden die helpen het Herzsprung Russel diagram van sterren te begrijpen.
 
 


 

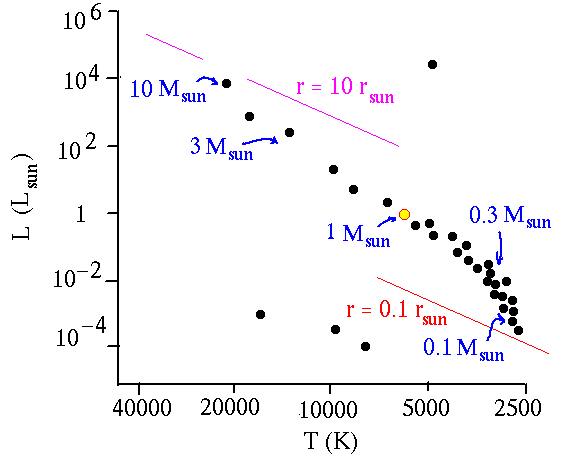
Figuur 1   Het Herzsprung-Russell diagram
 

Als we de vereenvoudiging maken dat de model ster een uniforme, constante dichtheid heeft kunnen we een aantal dingen afleiden.

Uit (1) kunnen we dan door van 0 -> R te integreren afleiden dat P(0) ~ M  / R
Uit (2) volgt dat P(0) ~  T(0)  zodat  volgt T(0) ~ M / R .
Verder kunnen we afleiden uit (3) dat L ~ R T(0)4 /  en  geldt natuurlijk dat  ~ M / R3  zodat volgt dat L ~  R4 T(0)4 /  M
Als we dan substitueren T(0) ~ M / R dan  volgt dat L evenredig is met  L ~ M3 / .

Dit is de massa - lichtkracht relatie voor sterren. In het Herzsprung-Russell (HR) diagram blijkt deze relatie L ~ M3.3 te zijn.

Verder kunnen we iets zeggen over de levensduur van sterren, m.a.w. de tijd dat de sterren in een stabiele fase zijn op de zogenoemde hoofdreeks (aangeduid door waar de sterren zijn getekend in figuur 1). Dit is de fase waarin in het sterinwendige waterstof door kernfusie wordt omgezet in helium.  Een eerste orde schatting van de levensduur krijgen we door de massa te delen door de uitgestraalde energie: m.a.w. levensduur t ~ M / L ~ M-2 ,  dus massieve sterren zijn kort op de hoofdreeks en lichte sterren lang.