Dubbelsterren

De massa's van sterren worden afgeschat uit de banen en bewegingen van dubbelstersystemen. Immers deze worden uitstluitend bepaald door gravitatie zoals beschreven door de wet van Newton en uit de bewegingen van sterren rond hun gezamenlijk massamiddelpunt is informatie te krijgen over de massa's van de sterren in een dubbelstersysteem.

Er zijn drie soorten dubbelstersystemen:

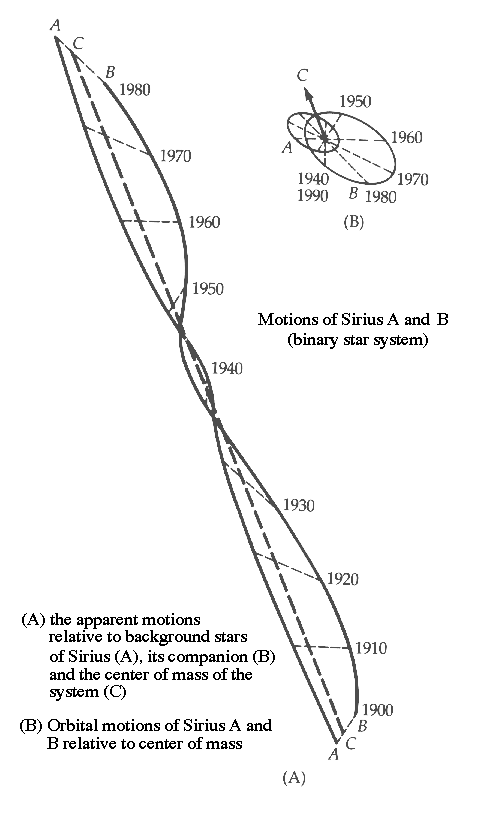
- de visuele dubbelsterren: systemen waarvan we beide sterren kunnen zien en dus ook de banen kunnen traceren. Een voorbeeld is de dubbelster Sirius, waarvan in de onderstaande figuur de relatieve banen zijn weergegeven zoals gemeten aan de hemel en zoals gemeten t.o.v. het massamiddelpunt van het systeem.
 


 

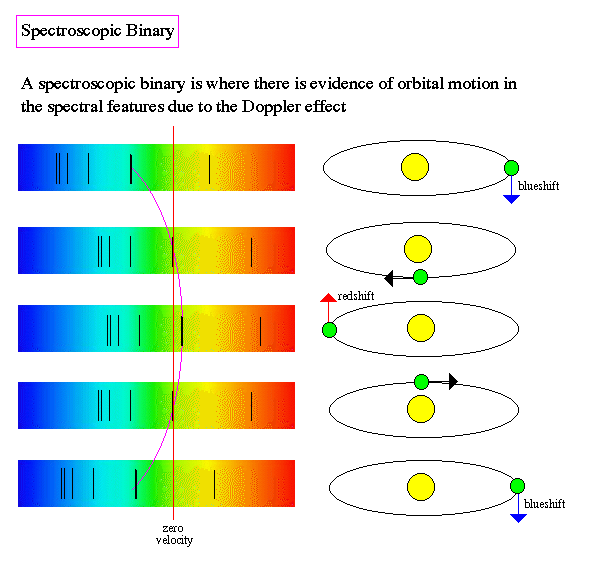
- de spectroscopische dubbelster: dubbelsterren die afzonderlijk niet te zien zijn, maar waar een van de sterren door verandering in de positie van spectraallijnen (t.g.v. het Doppler effect) verraadt dat ze onderdeel is van een dubbelstersysteem. De spectraallijnen geven de baan van de ster weer door periodieke oscillaties in golflengte. Onderstaande figuur geeft dit schematisch weer. In het geval van een visuele dubbelster kunnen we direct de derde wet van Kepler toepassen (p2 = 4 2 a3 / G ( m1 + m2 ))


 
 

Zie ook http://www-astronomy.mps.ohio-state.edu/~pogge/Ast162/Movies/specbin.html
        en http://www.eso.org/outreach/press-rel/pr-2001/pr-22-01.html
             http://astrwww.cwru.edu/Academic/luckastr211/Lectures/StellarMass/

In het geval van spectroscopische dubbelsterren meten we snelheden in plaats van posities via de Doppler verschuiving van de spectraallijnen. De waarneembare grootheden zijn:

de snelheid V van ster 1, de snelheid v van ster 2, en de periode P van de omloop van beide sterren om elkaar. Hieruit kunnen we de afstanden van beide sterren tot het massamiddelpunt uitrekenen. Immers:

V = 2r1 / P   zodat   r1 = V P / 2    , en ook:      r2 = v P / 2  .

Voor de halve lange as van de baan a  geldt dan  a =  r1  +  r2   .

Verder geldt voor de massa'a M en m van ster 1 en 2 :    M / n =  r2  / r1  = v / V

en kunnen we met behulp van de derde wet van Kepler ( P2 = 4 2 a3 / G ( M + m ) )  de massa'a berekenen.
 

Bovenstaande geldt voor een dubbelster met het baanvlak volledig langs de gezichtslijn. Als het baanvlak loodrecht op de gezichtslijn staat zullen we de bewegingen niet kunnen waarnemen aan de hand van het Doppler effect omdat ze geheel in het vlak van de hemel liggen en geen component langs de gezichtslijn hebben. Als we de hoek tussen het baanvlak en de hemel definieren als i  (de baan inclinatie) dan zijn de waargenomen snelheden V'  en  v'  gerelateerd aan de werkelijke baansnelheden  V en v  via:

V' = V sin ( I )   en    v' = v sin ( i )

voor de massaverhouding blijft gelden dat:  M / n =  r2  / r1  = v / V = v' / V'

zodat we nog steeds de massa' verhouding kunnen bepalen.  Kepler's derde wet wordt dan:

P2 = 4 2 a3 / G  sin( i ) ( M + m )

en als we de inclinatie niet kennen kunnen we de massa's nier precies bepalen. Dit is nog lastiger als we de spectraallijnen van slechts een van de sterren zien i.p.v. beide. Dan kunnen we alleen een zogenoemde massa functie f ( M, m ) definieren via:

( M = m ) P2 = a3 = (r1 + r2 )3 = r13( 1 + r1 / r2)3 = r13 (  1 + M / m )3 = (r1')3 ( M + m  )3 / m3 sin3 (i)

en  f ( M,m ) =  m3 sin3 (i) / ( M + m  )3  =  (r1')3  /  P2

We kennen de inclinaties doorgaans niet. Dit is geen probleem zolang we wqaarnemingen van veel dubbelstersystemen hebben en de banen willekeurigge orientaties thebben. We weten dat voor een willekeurige verdeling van banen get gemiddelde van sin 3(i)  0.59 is, zodat we dan toch een gemiddelde massa kunenn bepalen voor b.v. sterren van een bepaald type. Immers uit de spectra weten we ook iets van de ster types.
 
 

- de eclipsveranderlijken: dubbelsterren die niet afzonderlijk te zien zijn maar een baan hebben die langs de gezichtslijn valt zodat de sterren elkaar van tijd tot tijd bedekken. Dit leidt tot periodieke veranderingen in de gemeten helderheid als de ene ster zich voor de andere bevindt. Onderstaande figuur geeft dit schematisch weer. De periode is direct te herleiden uit de periode van de helderheidsverandering.
 
 


 
 
 

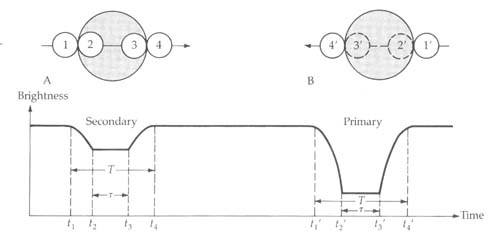
Uit de zogenoemde lichtkromme (de verandering van de helderheid met de tijd) van het systeem kunnen we een aantal eigenschappen afleiden. Waarneemgrootheden zijn (zie figuur hierboven):

de tijdstippen t1  t2  t3  en t4 , de periode P.

Geven we de sterren respectievelijk stralen Rs en Rp (waar s en p staan voor secondary en primary) dan geldt als de secondaire (kleinere) ster met snelheid v rond de primaire (grotere) ster beweegt:

2Rs = v ( t2  - t1  ) =  v ( t4  - t3  )   en   2 ( Rp + Rs ) = v ( t4  - t1  )

Ook weten we natuurlijk dat moet gelden:  a = v P / 2 

zodat we kunnen afleiden:

Rs / a =  ( t2  - t1  ) / P   en   Rp / a =  ( t4  - t2  ) / P