De Balmerserie komt
tot stand als electronen in het waterstofatoom terugvallen van hogere
``banen'' tot de een na laagste baan. We kunnen dit beschrijven met
behulp van een eenvoudig atoommodel: het Bohr atoom. Als we evenwicht
veronderstellen tussen de centripetale versnelling van een electron in
het electrostatisch veld van een proton en de Coulombkracht dan kunnen
we schrijven:
me v2 / r = Ze2 / r2
waar e de lading van het electron is (1.6 x 10-19 Coulomb) en Ze de lading van het proton, r de onderlinge afstand, me de massa van het electron 9.11 x 10-31 kg) en v de baansnelheid van het electron. Volgens Bohr's theorie van gekwantiseerde banen geldt dat:
me v r = n ( h / 2 p)
waarbij h de constante van Planck is (6.625 x 10-34 Joule s) en n een geheel getal (1, 2, 3, ....). Als we deze resultaten combineren vinden we:
r = Ze2 / me v2 = n h / 2pi me v = n2 ( h2 / 4p2 mee2Z)
Dus de Bohr banen komen voor op geometrisch met n2 toenemende afstanden tot de kern van een atoom. We kunnen nu de energie van de banen bekijken. We weten dat de totale energie de som is van de kinetische en de potentiele energie:
E = (m v2 / 2) - (Ze2 / r) -> E(n) = - (2p2mee4Z2)/n2h2
Nu zal bij terugvallen van het electron in een lagere baan een discrete energie in de vorm van een foton vrijkomen. De betreffende fotonenergie is hn. Stel het electron valt terug van baan n2 naar baan n1 , dan is de fotonenergie gelijk aan het verschil in de baanenergie tussen beide electronbanen. Dit betekent dat we de frekwentie van de betreffende lijnemissie kunnen schrijven als:
n12 = (E(n1) - E(n2))
/ h = (2p2mee4
/ h3) Z2 [ (1/n22) - (1/n12)]
Voor het waterstofatoom (Z = 1) kunnen we nu de frekwenties uitrekenen
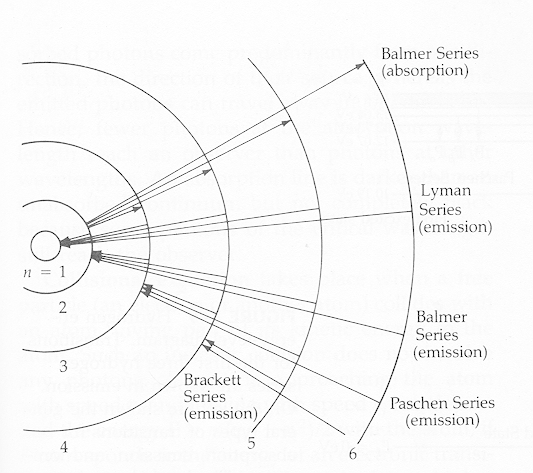
van de betreffende lijnovergangen. Figuur 1 geeft het simpele Bohr model
weer voor het waterstofatoom met de betreffende lijnenseries: de Lyman
serie, de Balmer serie, de Paschen serie en de Brackett serie in respectievelijk
het UV deel, het zichtbare deel, het rode deel en het infrarode deel van
het electromagnetische spectrum.
Emissie en absorptielijnen in andere elementen komen op een vergelijkbare
manier tot stand.

Figuur 1: Het Bohr model voor het waterstofatoom met daarin getekend
de onderste lijnseries. Als er sprake is van absorptie van een foton door
het naar een hogere baan brengen van een electron dan hebben we natuurlijk
te maken met een absorptielijn i.p.v. een emissielijn, zoals b.v. in de
fotosfeer van een ster.