|
|
Nederlandse Vereniging voor Weer- en Sterrenkunde
Naar
homepage
Secretariaat Nederlandse
Vereniging voor Weer- en Sterrenkunde NVWS: Drs. J.A. de Boer, Prinses
Irenelaan 1, 9765 AL Paterswolde. Telefoon 050 3094290 (na 19.00 uur), E-mail: J.A.de.Boer@rug.nl.
(Kamer van Koophandel voor
Utrecht en Omstreken V 477437)
|
|
|
Jan de Boer / 27 augustus 1999
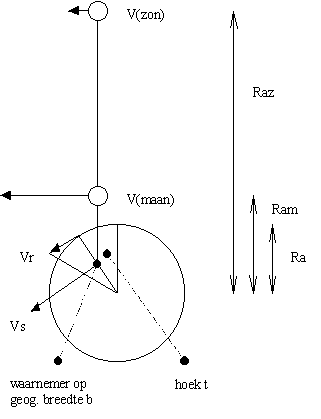
Grondsnelheid van de maanschaduw
In berichten in de pers en tussen amateurs
onderling lees je allerhande schattingen voor de grondsnelheid waarmee de
maanschaduw ons bij een totale eclips passeert. Laatst las ik nog 2000 km/h.
Mijn schatting is ruwweg 2200 km/h of hoger.
Met behulp van gegevens uit de
Sterrengids van de NVWS geven we hier een afschatting afgerond op een paar
honderd km/h van die snelheid. Geocentrisch is dat het beste duidelijk te
maken.
Zon (schijnbaar) en maan schuiven oostwaarts voor de sterren langs. De zon legt 360 graden af in een siderisch jaar (365.256 dg), de maan in een siderische maand (27.3217 dg). De maanbeweging domineert hier (13.37 maal sneller).
De maanbaan heeft een straal Ram
= 384400 km, dus een omtrek van 2415256 km. Afgelegd in 27.3217 dg is dat een
snelheid V(maan) = 3683 km/h (variatie van -200 tot +300 km/h door de baan-eccentriciteit).
Die beweging wordt schijnbaar afgezwakt door de oostwaartse zonsbeweging, er
kan ca. 275 km/h worden afgetrokken. Zie de factor 13.37, maar het volgt
preciezer uit (2 pi Raz/365.256*24) * (Ram/Raz), dwz. de snelheid van zon alsof
die op de afstand van de maan staat.
Hierna gebruiken we een
effectieve maansnelheid Vm = 3400 km/h (-200, +300). We verwaarlozen variaties
door afwijkingen van cirkelbanen. De snelheid door de ruimte van de maanschaduw
zou bij de aarde iets hoger zijn omdat de aarde Ram verder van de zon staat,
dat is ca. Raz/400, daarom verwaarlozen we dat effect. (Raz = 149.6 miljoen
km).
De grondsnelheid Vs van de
schaduw wordt meer dan Vm als we de eclips niet op het middaguur waarnemen. Vm
moeten we delen door de cosinus van hoek t. Waar de centrale lijn begint en
eindigt (t = -90 of +90 graden) gaat Vs naar oneindig. Nu hangt t samen met de
tijd waarop de waarnemer de totaliteit ziet: t = (T-12)*360/24. T is eigenlijk
de ware plaatselijke zonnetijd, maar voor een schatting op 100 km/h nauwkeurig
kun je de tijd van de tijdzone ook wel gebruiken maar dan wel het eventuele uur
zomertijd aftrekken.
De grondsnelheid wordt verder nog
verlaagd doordat de aarde met de schaduw meedraait. Aan de evenaar gaat dat met
Vr = 2pi*Ra/24 = 1670 km/h (Ra = 6378.1 km). Als de waarnemer op geografische
breedte b zit dan is de correctie kleiner: Vr*cos(b). We verwaarlozen
afwijkingen van de bolvorm voor de aarde.
We hebben dus de schatting Vs
= [3400/cos{(T-12)*360/24}] - 1670cos(b) (afronden op 100 km/h want 3400 is al
tussen +300, -200).
In Roemenië was T-12=0 en was Vs
dus ca. 3400-1670cos(45) = 2200 km/h. In Frankrijk was T rond 11:20