Voronoi Patterns & Geometric Scaling
Appendix to referee report
Revs. Mod. Phys. (Jones et al., 2003)
Appendix to referee report
Revs. Mod. Phys. (Jones et al., 2003)
Figure 1. A 3-D Voronoi tessellation of 1000 cells
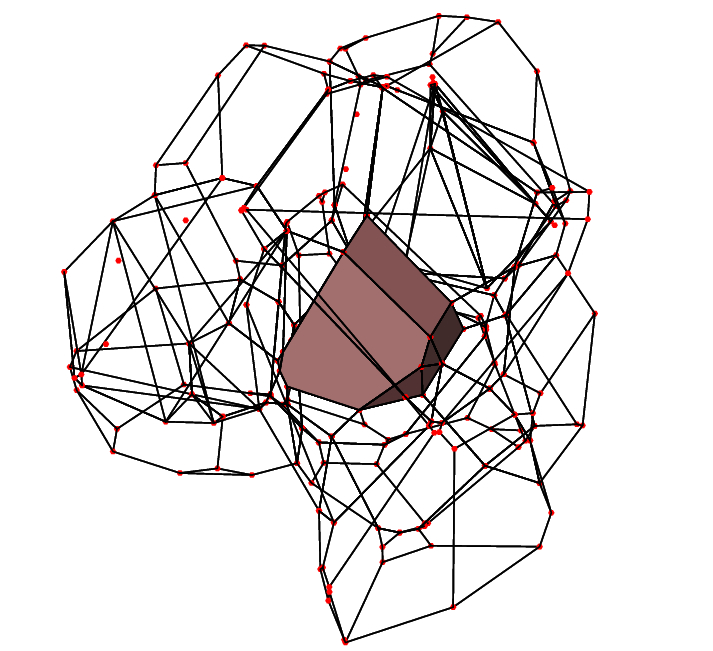
Figure 2. Wire diagram view of Voronoi cells,
edges indicated by solid lines, vertices by red dots
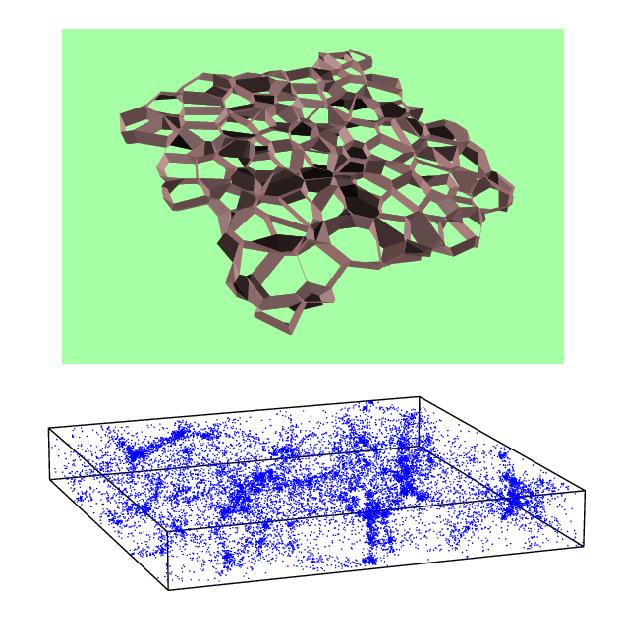
Figure 3. Slices through 3-D Voronoi tessellation:
top: geometric view
bottom: slice through Voronoi kinematic model particle distribution
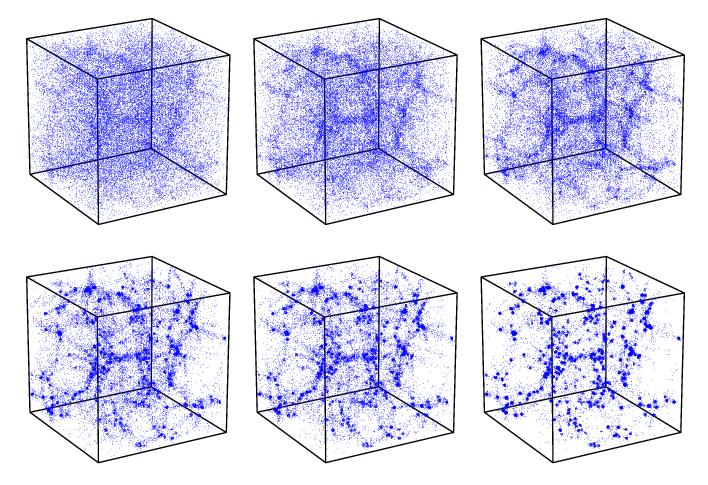
Figure 4. Evolution Voronoi kinematic model
particle distribution in Voronoi kinematic model at 6 successive timesteps
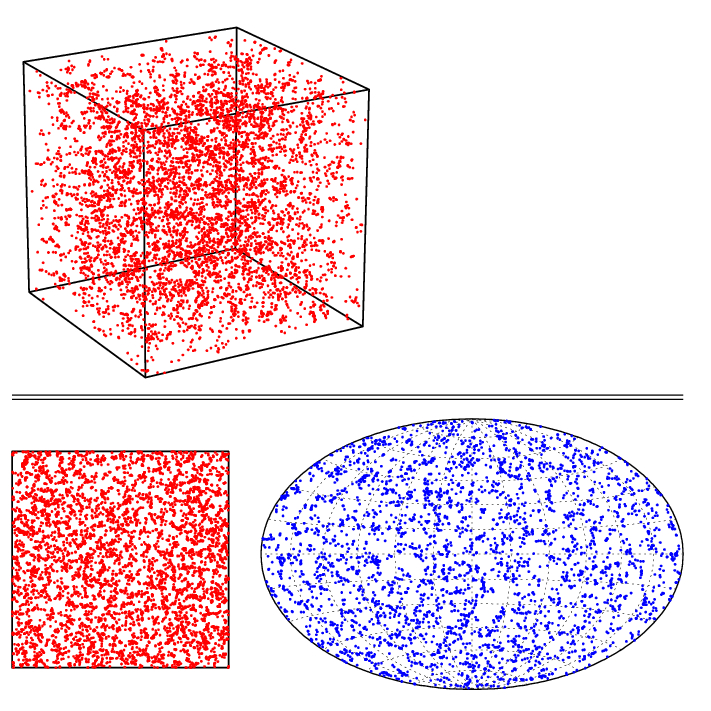
Figure 5. Voronoi vertex distribution
top: spatial distribution
bottom left: slice through 3-D distribution
bottom right: Aitoff projection of vertex sky distribution
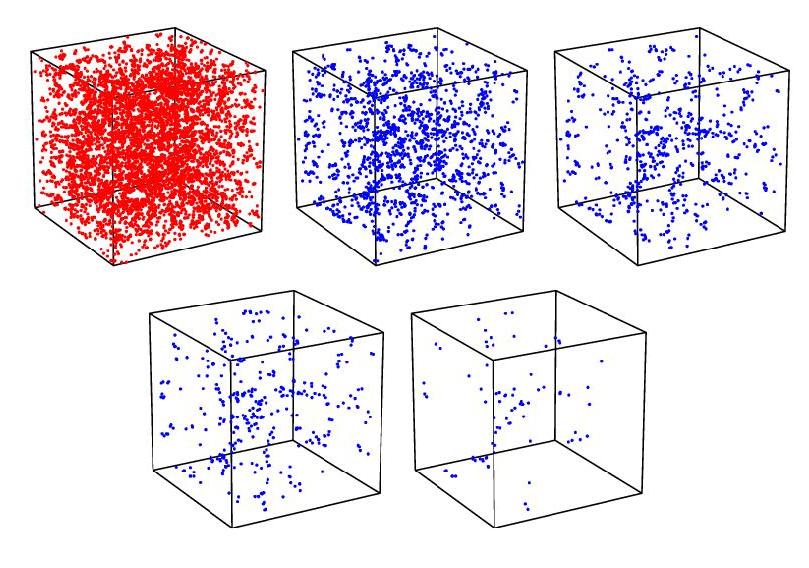
Figure 6. Voronoi vertex distribution bias:
spatial Voronoi vertex distribution for vertex samples,
selected at 5 successively richer "vertex mass" limits
(top left --> bottom right: complete sample, 25%, 12.5%, 5%, 1% richest
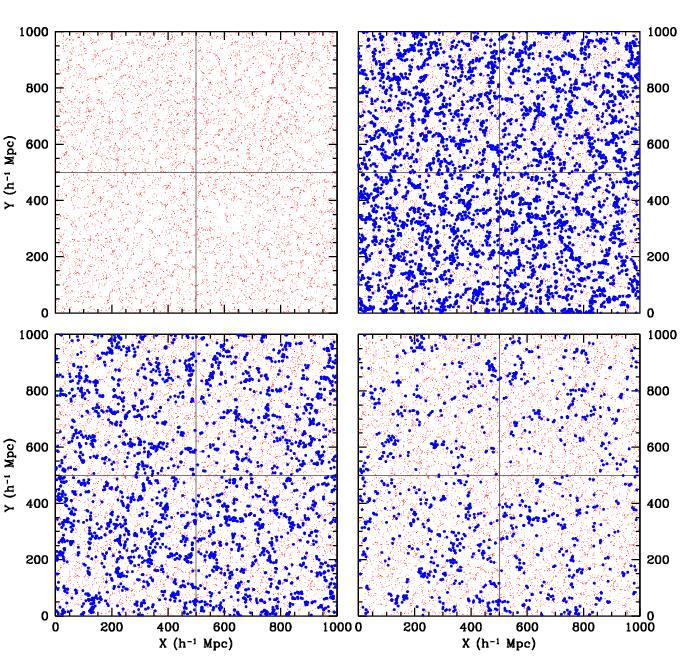
Figure 7. Voronoi vertex distribution bias:
Voronoi vertex distribution in central slice. Red dots: complete sample of Voronoi vertices
In three successive frames (top right, bottom left, bottom right) blue dots indicate
samples of 25%, 12.5% and 5% richest vertices
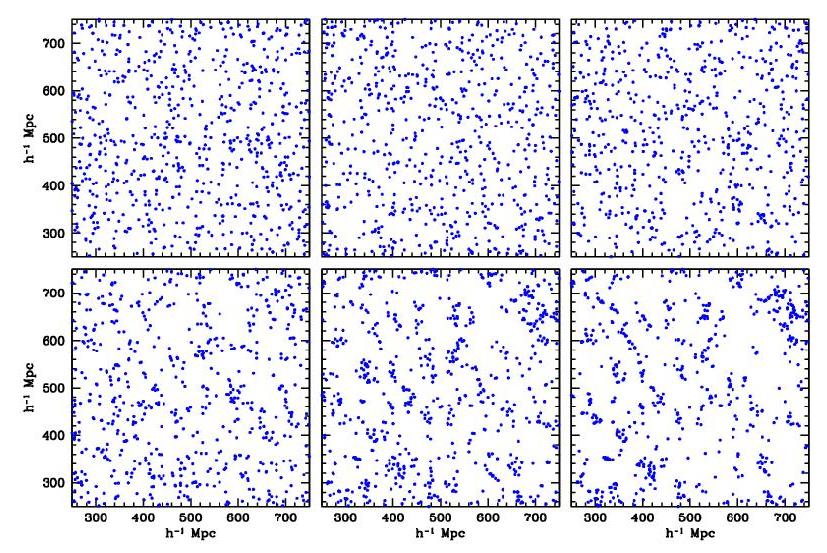
Figure 8. Voronoi vertex distribution bias:
6 samples of Voronoi vertices for 6 successive richnesses
(top left --> bottom right: full sample to 1% richest), scaled to equal number density.
Clear demonstration that differences in distribution not only due to number density but
also to differences in clustering properties
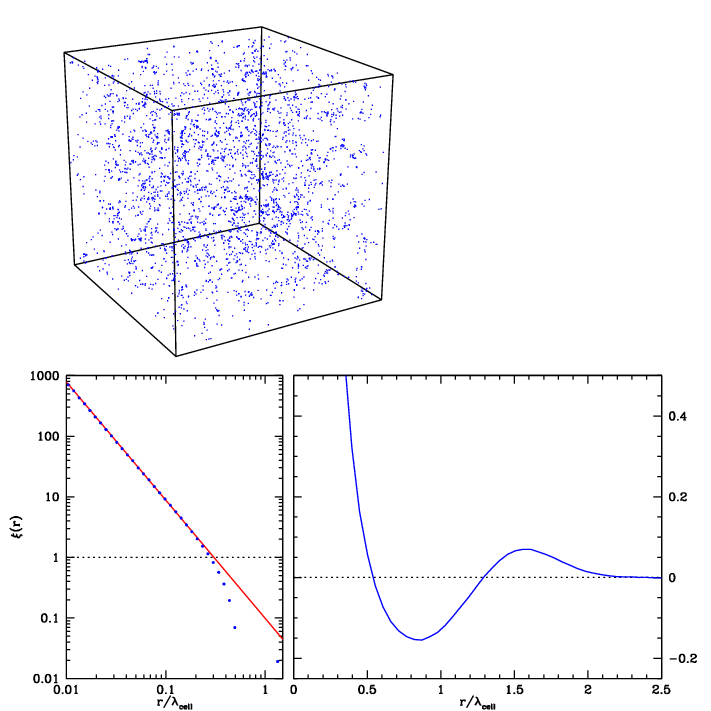
Figure 9. Voronoi vertex clustering
Two-point correlation function full Voronoi sample
top: spatial Voronoi vertex sample
bottom left: log-log plot xi(r); bottom right: lin-lin plot xi(r)
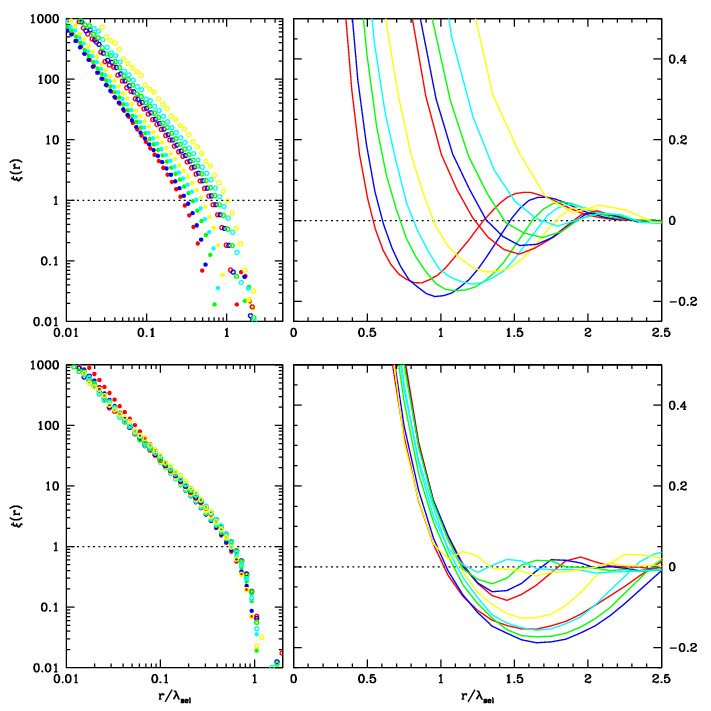
Figure 10. Voronoi vertex clustering
Two-point correlation function for samples of Voronoi vertices, a sequence of 10 samples of
successively richer (more massive) vertices:
top: log-log and lin-lin plots two-point correlation function, as function of true distance
bottom: same, but distance scaled to inter-vertex distance in samples
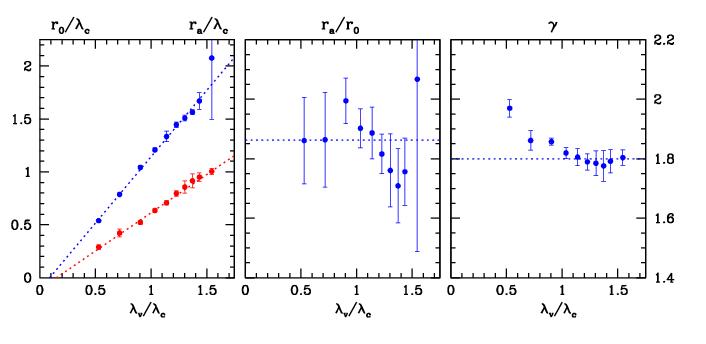
Figure 11. Voronoi vertex clustering: Geometric selfsimilarity ?
left: scaling of clustering length r_0 (xi(r_0)=1) and
correlation length r_a (spatial coherence length at which xi(r_a)=0),
as function of inter-vertex distance lambda_v (lambda_c is basic distance unit,
here equal to distance between tessellation nuclei)
centre: scaling ratio correlation length r_a/clustering length r_0 as
function inter-vertex distance lambda_v:
constant ratio indicates self-similarity Voronoi vertex scaling
right: scaling power-law index gamma of power-law regime correlation function xi(r)
as function of inter-vertex distance lambda_v
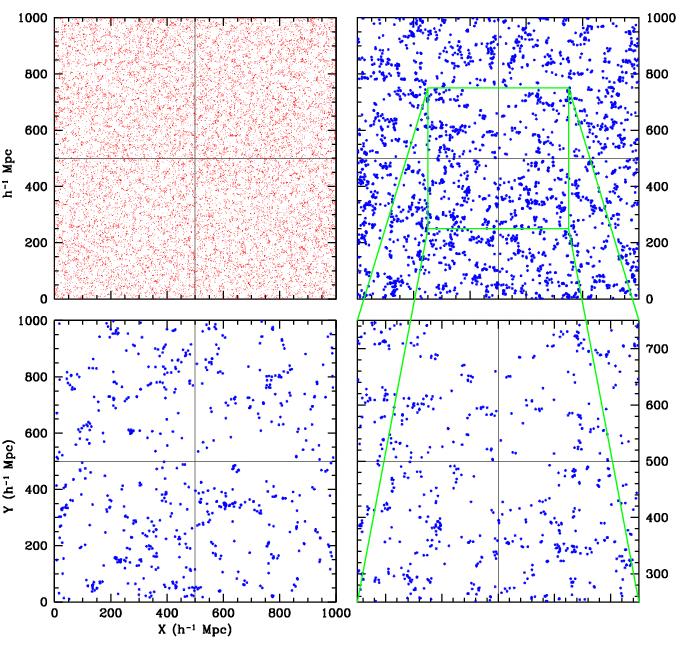
Figure 12. Significance geometric selfsimilarity:
Top left: slice through full sample Voronoi vertices (red dots)
Top right: selected 25% richest vertices from full sample,
green box: central box of 1/8 volume complete box
Bottom left: select 3.125% richest vertices from full sample,
Bottom right: vertex distribution green box inflated to same size, this scaling
yields spatial point distribution similar to that of 3.125% richest vertices