PIXELS, GRIDS & WORLD COORDINATES
This document is an analysis of GIPSY's (legacy) system of pixels,
grids and world coordinates. We describe a proposal to clean up the
existing code to make the system less sensitive to different definitions,
applied in the past.
A source of information are the minutes of the DEUK meetings,
The DEUK group consisted of a number of experienced
GIPSY users and programmers.
First some definitions:
Nearest integer
NINT() in (pre april 2009) GIPSY is either a function or a macro which rounds a
number to the nearest integer. In tasks written in C usually defined as:
#define NINT(a) ( (a) < 0 ? (int)((a)-.5) : (int)((a)+.5) )
This definition follows the definition of the Fortran NINT() function:
Returns a with the fractional portion of its
magnitude eliminated by rounding to the
nearest whole
number and with its sign preserved, converted
to type Integer
A fractional portion exactly equal to
`.5' is rounded to the whole number that
is larger in magnitude.
FITS pixel system
The FITS pixel system is a system where the first pixel is labeled 1 and
in a sequence of N pixels, the last pixel is labeled N. The system is an integer
system and the label corresponds with the center of a pixel.
|___|___|___|___|___|___|___|
1 2 3 4 N
CRPIX
CRPIX is an item from a FITS header and sets the location of the
reference point (CRVAL) of the axis. If CRPIX is an integer, the reference
is at the center of a pixel.
If CRPIX ends on .5, the reference is on the border
between two pixels.
GIPSY grid system
The GIPSY 'grid' system sets the pixel that corresponds to CRVAL to 0.
That pixel is set by the number of CRPIX. Values of CRPIX are not always
integer. Therefore we need to round its value. In GIPSY the NINT macro
is used for this rounding. The lower limit in grids is LO = 1 - NINT(CRPIX).
e.g. CRPIX = 3.3 then LO = 1 - NINT(3.3) = 1 - 3 = -2
|___|___|___|___|___|___|___|
-2 -1 0 1 N-2
The motivation for this choice was that it is convenient to have the
projection centre in/near (0,0) in transformations between image- and UV plane.
From DEUK meeting: deuk44.19jan90.txt:
PC
"Two symbols are proposed which denote one position. They are: PC (which
stands for projection centre and is effectively (0.0,...)) and AC (which
stands for axis centre and is effectively ((LHI+LLO-1)/2,..))."
AC
"It must of course also be possible to give a central position and a
size. The size is indicated by D (DELTA) followed by grids or physical
units. For example to select an area in an RA-FREQ map one could type:
AREA= AC D 0.5 DEGREE 500 KM/S"
The definition shows that at that time there was no special treatment
for CRPIX values that were not integer.
Detected inconsistency in the pre 01-04-2009 version of GIPSY
The definition of 'PC' and the implementation in the routines dealing with coordinate
transformations are different. One needs to include an offset caused by non-integer
values of CRPIX in the header of a set or FITS file.
In function cotrans.c the correction that has been applied for the value of 'PC'
is given in the code as:
set_info.ax[n].grid = set_info.ax[n].offset;
This offset is calculated with a call to a special function: offset(CRPIX)
which, in a previous version of cotrans.c is defined as:
static double offset( double x )
{
double r = x - floor( x );
if (r > 0.5) r -= 1.0;
return( r );
}
i.e.:
offset(-0.6) = -0.6 - floor(-0.6) = -0.6 - (-1) = 0.4 ==> r = 0.4
offset(-0.5) = -0.5 - floor(-0.5) = -0.5 - (-1) = 0.5 ==> r = 0.5
offset(-0.3) = -0.3 - floor(-0.3) = -0.3 - (-1) = 0.7 ==> r = 0.7 - 1 = -0.3
offset(0.0) = -0.0 - floor(0.0) = -0.0 - (-0.0) = 0.0 ==> r = 0.0
offset(+0.3) = +0.3 - floor(0.3) = 0.3 - (0) = 0.3 ==> r = 0.3
offset(+0.5) = +0.5 - floor(0.5) = 0.5 - (0) = 0.5 ==> r = 0.5
offset(+0.6) = +0.6 - floor(0.6) = 0.6 - (0) = 0.6 ==> r = 0.6 - 1 = -0.4
If the fractional part of CRPIX > 0.5 then the integer part should be increased with 1.
So CRPIX = 0.6 then the integer part is 1 and the offset is -0.4
and CRPIX = -0.6 then the integer part is -1 and the offset is 0.4
The integer values can be obtained by applying:
CRPIX_int = CRPIX - offset
This gives interesting values for:
CRPIX=-0.5: CRPIX_int = -0.5 - 0.5 = -1
and:
CRPIX=0.5: CRPIX_int = 0.5 - 0.5 = 0
The integer values of CRPIX are used to set the transformation between
the FITS pixel system and the GIPSY grid system.
Later, we found that this function behaved differently compared to the routines
which obtain boxes (axes limits in GIPSY grids) with macro NINT().
static double offset( double x )
{
return( x - NINT(x) );
}
In cotrans.c the NINT is defined as:
#define NINT(a) ( (a) < 0 ? (int)((a)-.5) : (int)((a)+.5) )
offset(-0.6) = -0.6 - NINT(-0.6) = -0.6 - (int) (-0.6-0.5) = -0.6 +1 = 0.4
offset(-0.5) = -0.5 - NINT(-0.5) = -0.5 - (int) (-0.5-0.5) = -0.5 +1 = 0.5
offset(-0.3) = -0.3 - NINT(-0.3) = -0.3 - (int) (-0.3-0.5) = -0.3 -0 = -0.3
offset( 0.0) = 0.0 - NINT( 0.0) = 0.0 - (int) ( 0.0+0.5) = 0.0 -0 = 0.0
offset( 0.3) = 0.3 - NINT( 0.3) = 0.3 - (int) ( 0.3+0.5) = 0.3 -0 = 0.3
offset( 0.5) = 0.5 - NINT( 0.5) = 0.5 - (int) ( 0.5+0.5) = 0.5 -1 = -0.5
offset( 0.6) = 0.6 - NINT( 0.6) = 0.6 - (int) ( 0.6+0.5) = 0.6 -1 = -0.4
Compared to the previous list one notices that the offset functions differ for
CRPIX=0.5.
With the same formula to obtain the integer part:
CRPIX_int = CRPIX - offset
one gets for:
CRPIX = -0.5: CRPIX_int = -0.5 + 0.5 = 0
CRPIX = 0.5: CRPIX_int = 0.5 - (-0.5) = 1
The CRPIX_int value is a measure for the translation from the GIPSY grid
system to the 1-based pixel system.
The conclusion then is that for (at least) CRPIX=0.5 one gets different values
for this shift between the grid- and pixel systems. Other functions that deal with
this conversion between systems (gds___unpack.c, gdsinp.c, gdsbox.c) use the
NINT macro. To prevent the mismatch we just described, it was decided to
replace the floor() based offset function by the NINT() based offset function.
We can make this more obvious in a plot where we compare the NINT macro
with C's floor() function in the offset function. It is obvious that the results differ for all
CRPIX > 0 for which the fractional part is 0.5.
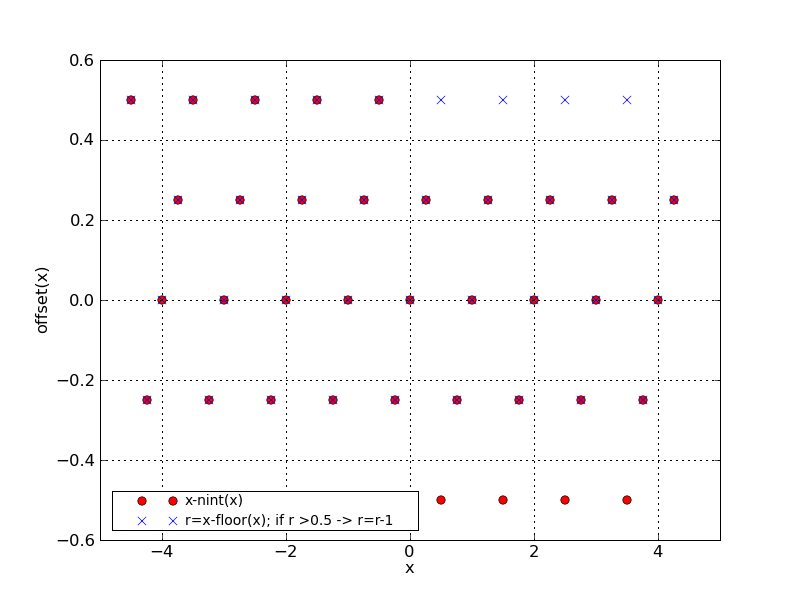
The problems arise when the fractional part of CRPIX is exactly 0.5 which results
in a one pixel shift of the grid coordinates. In practice there were numerous examples
of sets with CRPIX header values that fall into this category.
In some cases the choice seems to have a valid reason and in others it is probably a
mistake. The change in the offset function made the system more consistent but
less correct.
The behaviour of the NINT macro is point symmetric around zero. This causes
zero to be special point. There is no good reason why zero should be special.
The pixel system in FITS is starts to label pixels with '1' and the GIPSY coordinate
word system does the same. The motivation for the cotrans.c definition of
nearest integer is not documented, but private communications with
the original author of this function confirms that in fact negative values for
CRPIX were not taken in account, which seems valid for at least the majority of
FITS files, but invalid for sets processed by e.g. GIPSY tasks (e.g. all applications
that change the size of the output set with function gdscss.c.
In the next plot we show this and compare this
behaviour with the floor() function. The routines are evaluated for x in an
interval [-4.5, 4.5> in steps of 0.25.
In the plot it is shown that the floor and NINT macro differ for CRPIX < 0
when its fractional part is 0.5.
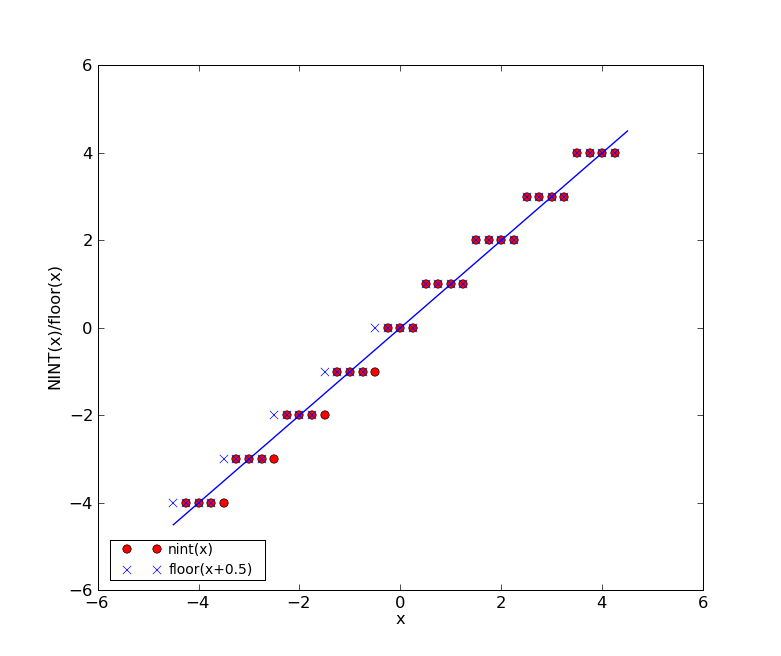
gds___unpack.c
Function gdsc_grids() calculates the grid values for coordinate word values of the limits
and uses function gds___unpack.c for this. The coordinate words in this routine
transform a coordinate word into a 1-based pixel system for each axis in a data set.
This rounding function in the unpack routine has a a different but
comparable definition of NINT.
#define NINT(a) ( (a)<0 ? (fint)((a)-.5) : (fint)((a)+.5) )
Just like the 1-based FITS pixel system, the coordinate word pixels start
to count with '1'. To return a GIPSY grid value it has to include the
value of CRPIX.
For a pixel position p it calculates the grid g with: g = p - NINT(CRPIX).
To calculate a lower axis limit 'blo' that corresponds with a FITS pixel position
equal to 1, we get for different values of CRPIX:
crpix = -2.5 ==> blo = NINT(3.5) = int (3.5+0.5) = 4
crpix = -1.5 ==> blo = NINT(2.5) = int (2.5+0.5) = 3
crpix = -0.5 ==> blo = NINT(1.5) = int (1.5+0.5) = 2
crpix = 0.5 ==> blo = NINT(0.5) = int (0.5+0.5) = 1
crpix = 1.5 ==> blo = NINT(-0.5) = int (-0.5-0.5) = -1
crpix = 2.5 ==> blo = NINT(-1.5) = int (-1.5-0.5) = -2
And here it becomes obvious that for CRPIX with a fractional part of 0.5
there is a jump from 1 to -1. For this fraction one cannot find a CRPIX
where the corresponding 'blo' is 0.
Conclusion: A grid coordinate system which converts from a 1-based pixel system
using the NINT macro as defined above, either excludes the use of CRPIX values
that have fractional parts equal to 0.5 or it excludes the existence of grid 0
for this category of CRPIX values.
Example: Application SLICE can extract a slice of data in a data cube
(e.g. RA-DEC-FREQ).
Then a set of sample points is defined in the spatial part of the data set.
One of the axes in the output set has a range [blo,bhi] = [0,0].
When the original CRPIX ends on .5 then after the creation of this output set,
there are no GIPSY applications that display the axis range correct
See also section: gdscss.c
With the NINT definition from above, is there a difference between:
g1 = p - NINT(CRPIX) and g2 = NINT(p-CRPIX) ?
Assume CRPIX=-2.5 and p = 1
g1 = 1 - NINT(-2.5) = 1 - (int) (-2.5-0.5) = 1 - (-3) = 4
g2 = NINT(1+2.5) = NINT(3.5) = (int) (3.5+0.5) = 4
This could be expected because of the symmetry of NINT in 0.
Only the 'jump' i
Later we will discuss the use of the floor function to get a nearest integer.
Then these two definitions to calculate g1 and g2 are not equal because
the floor function has no point symmetry in 0.
gdsbox.c
In gdsbox.c the NINT is used in the following definition:
#define NINT(x) ( x > 0.0 ? (fint) ( x + 0.5 ) : (fint) ( x - 0.5 ) )
which differs from the previous definitions but -again- gives the same results.
In gdsbox.c positions are calculated with the NINT macro.
For a central position and a size, it calculates the limits as:
fint
c = NINT( pos[k]
);
/* central position */
fint
s =
bhi[k];
/* size of box */
pos[k+subdim] = (double) ( c + s / 2 ); /* upper right */
pos[k] = pos[k+subdim] + (double) ( 1 - s ); /* lower left */
and somewhere else in the code:
fint c = NINT( pos[k] ); /* centre of box */
fint
l;
/* lower grid */
fint s = NINT( pos[k+subdim] ); /* size of box */
fint
u;
/* upper grid */
u = NINT( (double) ( c + s / 2 ) ); /* u-r */
l = NINT( (double) ( u + 1 - s ) ); /* l-l */
gdsinp.c
In gdsinp.c the upper and lower limits of set axes are set by the relations:
r.ax[n].low = 1 - NINT( crpix );
r.ax[n].upp = naxis - NINT( crpix );
which is based on the formula: g = p - NINT(CRPIX)
and the fact that the first pixel in FITS is '1'.
Further there is in gdsout (also in gdsinp.c) a routine to obtain a value
for CRPIX if we have to create a new set and have a (non integer) pixel value
for the lower axis limit. Then an iterative procedure tries to solve :
/* We want: NINT(set_info.ax[m].crpix) == ( 1 - low). */
That is, one requires: low = NINT(1-CRPIX) = 1 - NINT(CRPIX) and, given
a value for 'low', a new value of CRPIX is calculated with: NINT(CRPIX) = 1 - low
In the proposed iteration, the start value of CRPIX is copied from the original (e.g. from
the input set), a shift in integer pixels is applied and then an iteration is started
by increasing or decreasing the value by a small number.
So for those cases where low == 0 (where we proved that we could not find a CRPIX
that ended on .5) this routine could find a CRPIX very close (DBL_EPSILON) to the
original value.
If the NINT() macro is replaced by a definition with C's floor() function, then probably
this iteration needs not to be applied anymore. To be save we should not clean up the
iteration code, because it is difficult to predict whether the iteration is necessary in
other circumstances.
gdscss.c
Another function in gdsinp is gdscss.c It changes/sets the axes limits in an output
set.
out_buf[k].ax[n].naxis = bhi[n] - blo[n] + 1;
out_buf[k].ax[n].crpix += (double) ( out_buf[k].ax[n].low - blo[n] );
out_buf[k].ax[n].low = blo[n];
out_buf[k].ax[n].upp = bhi[n];
With these relations we can show that there is an inconsistency in the transformations
with the NINT macro. Here is a recipe:
1) The NINT is defined as: x = NINT(a) ==> a > 0 x = int (a + 0.5) else x = int (a - 0.5)
2) The lower axis limit is defined in blo = 1.0 - NINT(crpix)
3) Assume CRPIX = -3.5 then blo = 1 - NINT(-3.5) = 1 - int (-3.5-0.5) = 1 - (-4) = 5
4) In gdscss a new CRPIX is calculated using the old value and then a value
is added which depends on the new blo, the lower axis limit:
out_buf[k].ax[n].crpix += (double) ( out_buf[k].ax[n].low - blo[n] );
or: crpix_new = crpix_old + (blo_old - blo_new)
5) Assume we want blo_new = 0 as output and use this value in gdscss. The new CRPIX
becomes:
crpix_new = -3.5 + (5 - 0) = 1.5
6) Is this the CRPIX that gives the right blo according to another formula used
in gdsinp:
blo_check = 1 - NINT(crpix) = 1 - NINT(1.5) = 1 - int(1.5+0.5) = 1 - 2 = -1
7) Conclusion : blo_check != blo_new
This problem can be avoided by using C's function floor(x+0.5).
Let's follow the same recipe:
1) Replace NINT(x) by floor(x+0.5)
2) The lower axis limit is defined in blo = 1.0 - NINT(crpix)
3) Assume CRPIX = -3.5 then blo = 1 - floor(-3.5+0.5) = 1 - (-3) = 4
4) In gdscss a new CRPIX is calculated using the old value and then a value
is added which depends on the new blo, the lower axis limit:
out_buf[k].ax[n].crpix += (double) ( out_buf[k].ax[n].low - blo[n] );
or: crpix_new = crpix_old + (blo_old - blo_new)
5) Assume we want blo_new = 0 as output and use this value in gdscss. The new CRPIX
becomes:
crpix_new = -3.5 + (4 - 0) = 0.5
6) Is this the CRPIX that gives the right blo according to another formula used
in gdsinp:
blo_check = 1 - floor(crpix+0.5) = 1 - floor(0.5+0.5) = 1 - 1 = 0
7) Conclusion : blo_check == blo_new
What we change after the introduction of function floor() is the behaviour of
the transformation from pixels to grids at the border of the pixels.
With floor() the left border of each pixel (in the 1-dim. case) belongs to the pixel
itself. The right border belongs to the next (right) pixel. With the NINT macro
this border behaviour is symmetric around 0 which gives the unwanted behaviour
for blo_new = 0.
Function floor() and the transformation between grids and pixels
For FITS pixels or coordinate word pixels that start with '1' we can calculate
the value of the lower limit of an axis in two ways:
g1 = p - floor(CRPIX+0.5) and g2 = NINT(p-CRPIX+0.5) ?
Assume CRPIX=-2.5 and p = 1
g1 = 1 - floor(-2.5+0.5) = 1 - (-2) = 3
g2 = floor(1+2.5+0.5) = floor(4) = 4
These conflicts do not arise for CRPIX values that do not have a fractional part
equal to 0.5. To get a consistent system we have to decide which formula is
correct. In the next figure we plotted values for g1 and g2 for a
range of x values in steps of 0.25.
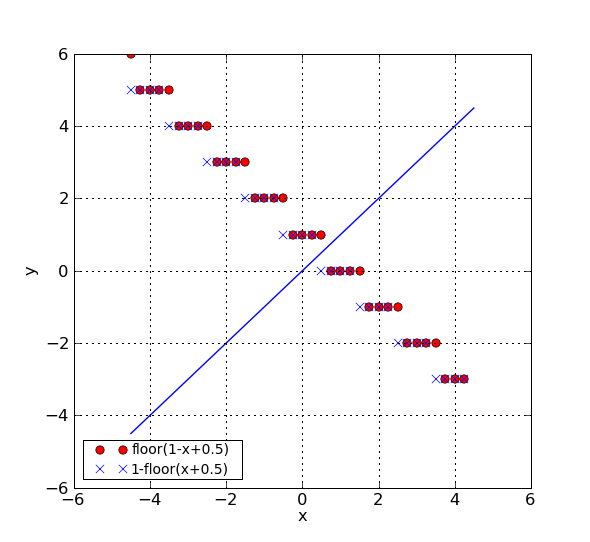
The formula should be consistent with the requirement that we want to include the
left border in the pixel. Then for CRPIX = -2.5 we want the same grid as for
CRPIX=-2.4 (i.e. 3). This can only be obtained by the first definition.
Conclusion: When floor(x+0.5) gets the role of the macro NINT then it is important
for consistency how the transformation from pixel to grid is defined.
The proposed formula is:
grid = pixel - floor(CRPIX+0.5)
Definition of 'AC'
For 'AC' the centre of a data set:
set_info.ax[n].grid = 0.5 * ( set_info.ax[n].naxis + 1.0 )
- set_info.ax[n].crpix + set_info.ax[n].offset;
This also differs from the original definition from the same deuk document.
MathWorld definition of nint()
The nearest integer function nint(x) of 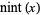 , illustrated above
and also called nint
, illustrated above
and also called nint
or the round function, is defined such that ![[x]](https://mathworld.wolfram.com/images/equations/NearestIntegerFunction/Inline2.gif) is the integer closest to
is the integer closest to 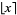 .
.
Since this definition
is ambiguous for half-integers, the additional rule that
half-integers are always
rounded to even numbers is usually added in order to
avoid statistical biasing. For
example, ![[1.5]=2](https://mathworld.wolfram.com/images/equations/NearestIntegerFunction/Inline4.gif) ,
, ![[2.5]=2](https://mathworld.wolfram.com/images/equations/NearestIntegerFunction/Inline5.gif) ,
, ![[3.5]=4](https://mathworld.wolfram.com/images/equations/NearestIntegerFunction/Inline6.gif) ,
, ![[4.5]=4](https://mathworld.wolfram.com/images/equations/NearestIntegerFunction/Inline7.gif) , etc.
, etc.
This
convention is followed in the C math.h library function rint
We examined the all the routines dealing with coordinate transformations
and defined 4 categories of code:
1. NINTs in functions
*gdsbox.c: All NINTs are used for positions
*cotrans.c: NINT only used in an offset function
*gdsinp.c: NINT only used for coordinate transformations
*gds_unpack.c NINT only used for coordinate transformations
*gdspos.c NINT defined but not used
A related function is gds_extend. This routine defines the origin of an axis
and uses CRPIX for this. The routine is called in gdsinp.c and several
tasks that build a new set. All these calls use CRPIX to define the origin
of an axis. There is no need to change this function because there are no
NINT's involved.
Less important functions:
*fie.c
Provides
a NINT for expression evaluation. According to the
source code it behaves like the classic NINT macro,
but it is
defined as a function.
*dms.c
Fred
Lahuis version of nint. No coordinates involved. Do not change.
*drawaxis.c Deals with coordinates. Tasks gplot.src and sliceview.src depend
on this function.
*ellipsefill.c NINT for positions. Do change.
*fillgauss2d.c Two NINTs for coordinates. Do change
*gauestd.c Uses NINT in coordinate like calculations. Do change.
*herinp.c dcd_nint defined. The routine herinp.c seems not to be used
in other sources.
*hms.c
Fred
Lahuis version of nint. No coordinates involved. Do not change.
*interpol.c NINTs used to find image value in interpolation routine.
No need to change because the interpolation
is also correct for
values on the
border of pixels. Do not change.
*scanline.c NINTs used for coordinates. Do change.
2. nint() in functions
*pgdriv.src nint() not for coordinates. nint() here defined as floor()
*gdsd_wfits.shl nint() only used to distinguish floats and doubles
from integer. Therefore harmless and there is no need
to change the code.
*irpl_snip.shl nint() only used to convert a sqrt to integer.
Do not change
*dydx.src Harmless. Only used to set derivative to 0. Do not
change.
Proposal:
For the functions in 1. one can change the current macro
#define NINT(x) ( x > 0.0 ? (fint) ( x + 0.5 ) : (fint) ( x - 0.5 ) )
into:
#define NINT(a) ( (int) floor( (double) (a) + 0.5 ) )
This will not interfere with other use of the NINT macro.
For category 2. there is nothing to do.
3. NINTs in C tasks
*antpat.src Unused NINT()
*funplot.src NINT used only in a list of supported functions.
Depends on function fie.c
*gdsserver.src NINT defined but not used.
*gids.src It defines (yet) another version for the nearest integer.
int misc_nint( double d )
{
int r;
if
(d > 0) r = d + 0.5; else { r = -d + 0.5; r = -r; }
return( r );
}
It is not used for grid coordinates so we leave it
unaltered.
*gaufit2d.src NINT() defined but not used
*cola.c NINTs for coordinate transformations only
-hermes.src NINTs for coordinate transformation and 1 other situation
*gplot.src Some NINTS for positions
*pyblot.src A Python program using the Fortran definition of nint().
*qplot.c NINT 1 time for a coordinate
*regrid.c NINT two times for a coordinate involving cdelt not crpix
*reproj.c NINTs used for coordinates
*rotmas.src NINT defined but not used
*sliceview.src NINTs used for coordinates
*trace.c NINTs for positions
*wfits.c NINTs for scaling numbers in the data. Not coordinates.
We leave this application unaltered.
*xgaufit.src NINT defined but not used
*xgauprof.src NINT defined but not used
4. nint() in tasks
*ellfit.c nint() for positions. nint() as a real function
*gmarker nint() for positions. Used as macro equivalent to NINT
#define
nint(f)
(f>0.0?(fint)(f+0.5):-1*((fint)(0.5-f)))
-hermes.src nint_i() use unknown (with 'dangerous' in its comment).
No need to change (J.P.T)
*reswri.c nint() used for coordinates. Used as macro NINT
*rfits.c Use of function nint(double). All related to coordinates.
*tracks.c IRAS. nint() used for coordinates. nint(a) == ( (int)( (a) + 0.5 ) ) which
behaves only as floor() for x > 0.0. The macro is used for
world coordinates only. Do not change.
5. NINT() in Fortran tasks
*combin.shl Only nint in documentation. It depends on fie.c
*create.shl Only nint in documentation. It depends on fie.c
*galmod.f Uses Fortran IDNINT(real*2) for setting the integer
value of crpix3 and therefore should only be
important
for velocity axes with
negative half integer crpix.
More
research needed. Low priority.
*ipaccal.src IRAS. Fortran nint() not used for coordinates.
*points.src IRAS. nint defined but not used
*plate.src IRAS. nint not used for coordinates. There is one with
nint(crval) but this are world coordinates.
*render.src NINTs used for internal positions. Probably not dangerous
*zodycal.src Is a Fortran program. nint() used for world coordinates
not grids. Do not change.
Proposal:
The NINT's from cola.c are used in a way similar to gdsbox() and must be updated with
the same priority as gdsbox.c. For other tasks it is important to update when
transformations are involved (reproj.c, sliceview.src). For those where NINT
is used to calculate positions the priority is lower, but they should also be
updated for consistency.
In rfits.c the pixel to grid transformation is needed to be able to prompt the
user with a default for the axis limits. Program gmarker.c , reswri.c and ellfit.c
should be updated for consistency. These last three applications do not propagate
coordinates so the priority to update them is not high.
From grids to world coordinates
Another problem is related to the use of proco.c in some tasks (e.g. reproj.c).
In reproj.c there is a conversion between grids and world coordinates using the function
proco.c. This routine does not take non integer crpix into account and therefore
does not convert properly.
This becomes obvious in cotrans.c. Here an offset function is defined which corrects
GIPSY grids for the fractional parts of CRPIX.
#define GETGRID( n ) \
set_info.ax[n].grid - set_info.ax[n].offset
#define SETGRID( n ) \
set_info.ax[n].grid += set_info.ax[n].offset
The offset function has been discussed in a previous section. If one wants to convert
grid position 0,0 to world coordinates and the fractional part of CRPIX is not 0.0 then
0,0 does not present the projection center. This is important to know: 0,0 only indicates
in which pixel the projection center is, but not exactly where in that pixel. Remember that the
transformation between (FITS) pixels and GIPSY grids is an integer translation.
Only when transformations from and to world coordinates are involved we have to be
careful (e.g. when using proco() instead of cotrans()).
Assume we have CRPIX = 3.4, then the offset = 3.4 - floor(3.4+0.5) = 0.4
The center of grid 0 is at distance -0.4 from the projection center. This is the value in grids we
have to supply for the projection transformation function proco(). The function itself
has no information about CRPIX or offsets. Therefore functions and applications
that use proco() for their transformations to or from world coordinates, need to apply
a correction like cotrans().
So the offset is defined as:
offset = CRPIX - floor(CRPIX+0.5)
and a grid for proco() should be corrected with an offset:
grid_proco = grid - offset
which implies that after a transformation from a world coordinate to a grid,
one should add the offset:
grid = grid_proco + offset
A projection center in cotrans() entered as 'PC' is first calculated with
grid = 0.0 + offset and then: grid_proco = grid - offset = 0.0+offset-offset = 0.0
Applications cplot.c, dssload.c, reproj.c, slice.c all use proco() without this correction.
This can be fixed independently from the change of macro NINT.
Functions drawaxis.c and skypro.c use proco() but the first corrects already for offsets
and the latter is used in the context of cotrans() only and cotrans() applies the offset
correction already. In drawaxis() the NINT macro is used to calculate the offset.
This macro should be replaced by the one containing the floor() function.
Another important application is copy.shl. It is written in Sheltran and it also deals with
coordinates (gdscss()). The code itself does not contain any references to macro NINT so
after the update of gdsinp.c the program will work correctly.
What has been done?
09-04-2009: Application slice.c has been updated. The output grids in proco() needed to
be corrected the fractional part of CRPIX. The input grids were left unmodified.
They represent correct positions w.r.t. the selected rotation center.
11-04-2009: Application reproj.c is adapted for tne new macro for NINT. More important,
the coordinate transformation in function transform() is corrected for non
integer values of CRPIX. Before this change, all rotations around the projection
center were effectifely rotations around (0,0).
11-04-2009: gdsbox.c, cotrans.c, gdsinp.c, gds_unpack.c, gdspos.c
Changed definition of NINT, and tested all changes (with half integer
values of CRPIX). The reported exception in gdscss() (part of gdsinp.c)
doed not occur anymore. The iteration with DBL_EPSILON in gdsinp.c
triggered on positive half integer values of CRPIX. After the update to
the new definition of NINT() we did not find any iterations anymore
(for a suite of CRPIX values). The updated code seems more consistent.
12-04-2009: cola.c, rfits.c, only the definition of NINT was changed.
Program header.c had a hidden problem. It calculates the grid that corresponds
to the projection center but it did not calculate the offsets correctly
((int) instead of NINT). This has been restored with the new macro of NINT.
Header now displays the same offsets as program coords (with POS=PC).
Program sliceview.src uses macro NINT for positions. For consistency in
the definitions of coordinates the macro has been changed to the new definition.
The program uses routine grtoph() and phtogr() for the conversion between
grids and world coordinates. It does this in the context of cotrans.c which keeps
track of non-integer values of CRPIX and calculates the right offsets for
the position of the projection center. Plot program cplot.c has the same
problem as the applications reproj.c and slice.c i.e. there is no correction for
non integer values for CRPIX before and after a call to proco(). This problem
has also been corrected in this April 12 release.
14-04-2009: Changed NINT definitions in gplot.src, qplot.c, regrid.c, trace.c.
Cleaned up the code in render.src, but the use of NINT() in the Fortran
code was not changed. Note that the Fortran NINT() behaves exactly the
same as the C NINT() macro. However, the core of render (which is Fortran)
does not use NINT() for coordinate conversions and therefore we left the
core unaltered.
Program antpat.src was cleaned up a bit. Macro NINT() was not used and therefore
deleted.
Function fie.c defined a nearest integer function called fie_nint() which behaved like
the old version of NINT(). It was changed to the floor() version. After that,
program funplot.src could be tested. This program is based on the expression
evaluation of fie.c.
In application gaufit2d.src the NINT() macro was defined but not used, so we
removed it.
Function drawaxis.c plots labeled frames around images and has a close relation
to coordinates involving CRPIX. The NINT() macro was used to calculate offsets
similar to cotrans.c. With this latest update, it is compatible with cotrans.c.
A bug was removed also. The grid offsets were initialized to 0 in a loop.
Then always one of the offsets was wrong. Now also sliceview.src is consistent.
The mouse positions are calculated with grtoph() and the axis labels with proco()
and they are equal now for all values of CRPIX.
15-04-2009: Changed nint() definition in reswri.c. This macro is only used to
get values of a box and therefore could be inconsistent with functions that
deal with coordinates. Two includes were missing and an 'or' statement was wrong.
Both problems were fixed.
In pyblot.src (Python source) we changed the definition of nint() because it is used
in the context of coordinates.
Macro NINT was removed from xgaufit.src, xgauprof.src and rotmas.src.
These last three application were also cleaned upo a bit (missing includes) and
from rotmas.src a bug with an uninitialized string was removed.
Changed NINTs in herinp.c, fillgauss2d.c, ellipsefit.c, gauest.c, ellipsefill.c,
interpol.c, scanline.c
The application ellfit.c uses a NINT for coordinates and therefore we changed its
definition. Regretably this application only works with a worning version of GIDS.
The same remarks apply to gmarker.c.


