As a contribution to the face-to-face meeting of Opticon N3.6 in March 2007, we compiled this document which describes how task parameters are handled in GIPSY, the Groningen Image Processing SYstem. A significant part of the ideas behind the parameter system originate from the seventies of the previous century and continue to be useful until this date. Nowadays scripting languages like Python are available which can facilitate the parsing and processing of parameters, but an integrated facility remains valuable.
In this document we first describe the basics of the parameter interface, giving a global view of its architecture and operation, and the interaction between the user, the user interface and the tasks. In later chapters we give a more detailed description of how the user can specify parameter values.
Central in GIPSY's parameter handling is the user interface Hermes, which is run as a separate process. Hermes allows the user to run one or more tasks concurrently, control these tasks and supply parameters to these tasks. Every task has its private set of parameters which is stored as a collection of keyword-value pairs. The value is always stored as a text string; when the task requests the parameter, it can specify what type of parameter it expects, e.g. an array of floating point numbers or a logical value. Hermes then checks the value and if it is valid, it decodes the text string and sends binary values to the task. If the value is invalid (for the requested type), it is 'rejected' and the user is prompted to correct the value. This is all transparent to the task: only when a correct value is available, it is allowed to proceed.
If a task requests a parameter that has not been specified yet, the user
will be prompted to enter a value, or, if the task allows this, a default
value will be taken.
Subsequent requests for the same parameter silently causes the current value
to be sent to the task - the user is not prompted. Note that this current
value may have changed since the last request.
This is different when the task has 'cancelled' the keyword.
Then the user will be prompted for that keyword.
In this way a task can obtain a sequence of values for the same keyword.
Such a sequence can also be pre-specified on the Hermes command line using a
special syntax or can be obtained from a text file.
The user can modify a task's parameters at any time. The change becomes effective when the task requests the parameter from Hermes, which some tasks do very frequently. Also tasks can modify parameters, their own but also the parameters of other active tasks. In this way tasks can communicate with each other.
After a task has run, the task's parameters are retained by Hermes. The user can then re-run the task with the same parameters, possibly after having edited them or modified on the command line.
Finally, there is the possiblity to specify parameter defaults for a specific task or for all tasks in a special file.
Transferring parameters to a task is done through keywords. When a task needs information, Hermes will prompt the user on the task's behalf with the keyword and an explanatory message. A keyword is a case-insensitive character string followed by an equal sign (e.g. INSET=). Following the equal sign, one or more values can be given. Depending on the function of the keyword these values can be floating point numbers, integers, character strings and also expressions.
Here is an example how to start a task (INSPECTOR) with two keyword values (keywords INSET= and BOX=)
- 17:01 - 26 - - INSPECTOR INSET=lmap_uni.vs2.cl FREQ 20:30 BOX=0 0 D 20 20__________________ ______________________________________________________________________________
A prompt for a parameter appears on the command line of Hermes as the name of the task followed by the parameter's keyword, together with a short description of the input and a reasonable default e.g.:
- GAUSS Enter name of profile axis: [FREQ] 17:07 - 31 - - GAUSS PROFILE=_________________________________________________________________ _______________________________________________________________________________
The programmer defines the keywords of a task, the order of appearance and the order of processing the keyword values. A program can guide the user through the keyword list with defaults that are sensitive to the context (e.g., the data set being processed, the values of previously entered parameters, etc.)
Parameter processing in tasks with a graphical user interface, which are event-driven, is exactly the same as in tasks without a GUI. In such tasks the elements of the GUI are usually associated with a parameter keyword. Such an associated element always reflects the parameter's value. On the other hand, when the user changes the element, the parameter value is updated. When the parameter value changes, the task will receive an event. It is these events the task's application code reacts to, not the events from the GUI elements themselves. Prompting by Hermes is not possible for tasks with a GUI because this would cause the GUI to 'freeze' until the input is given.
Hermes can provide context-sensitive information about a task's parameter request at a single keystroke (the TAB key). This help is extracted from the documentation of the task. With the keystrokes ESC TAB the user gets a description of the keyword category with examples and some detailed request information. At the prompt 'INSET=', typing ESC TAB causes the following text to be displayed:
INPUT OF SET (AND SUBSETS)
==========================
Example: The structure AURORA is 3-d and has axes RA,DEC and
FREQ with sizes:
RA from -63 to 64
DEC from -63 to 64
FREQ from 1 to 32
.
.
.
INSET=AURORA RA 0 DEC 0 FREQ 1
gives a pixel at (RA, DEC, FREQ) = (0, 0, 1)
See also: INPUT SYNTAX FOR SETS [1]
-----------------------------------------------------------
Detailed request information:
Up to 512 characters. See also: text input [2].
No default is available.
The bracketed numbers in this help display allow the user to navigate to other documentation about parameter input. E.g., typing ESC 2 will show information about text input.
The basic input parameter types are:
Three default levels are supported:
Numerical parameters can be specified as numeric or symbolic constants and also as expressions. Expressions can be built from operators, numbers, constants, variables and functions.
A list of numbers can be specified as a sequence separated by spaces or using the start:end:increment notation, where the :increment part is optional and defaults to one. A list of n identical values can be specified as value::n.
A list can also be used as an operand in an expression or as an argument to a function. In the former case the list must be enclosed by square brackets [ ] or parentheses ( ). The expression is evaluated for each element of the list.
The operator ? can be used to select one or more items from a list.
Examples:1 2 3/3 sin(pi) yields 1.0 2.0 1.0 0.0 log(10)::4 yields 1.0 1.0 1.0 1.0 log(10):log(100):2/4 yields 1.0 1.5 2.0 10**[0 1 5] yields 1 10 100000 [1:3]+[90:70:-10] yields 91 82 73 [20:30]?[3 4 5] yields 22 23 24 ranu(0,1)::10 yields 10 copies of the same random number ranu(0,1::10) yields 10 different random numbers
Suppose an inclination at keyword INCL= must be given in degrees, but you want to give the input in axis ratio.
INCL= deg(acos(0.3 0.5))
The argument for acos is a list consisting of the elements 0.3 and 0.5. The expression evaluates these two values for acos and converts the resulting values to degrees. In this way the values 0.3 and 0.5 are converted to the angles 72.5424° and 60.0°.
The following list gives an overview of the elements that can be used:
numbers: Numbers can be specified as integers, using fixed point
notation or using E or D format. Internally all numbers are
represented as double precision floating point numbers.
e.g. 123 123.45 1234.5E-2 .12345D3
operators: The following operators are known:
+ addition - subtraction
* multiplication / division
** power
constants: The following constants are implemented:
pi 3.14159.... c speed of light (SI)
h Planck (SI) k Boltzmann (SI)
g gravitation (SI) s Stefan-Boltzman (SI)
m mass of sun (SI) p parsec (SI)
BLANK Universal undefined value
functions: The following mathematical functions are implemented:
abs(x) absolute value of x
sqrt(x) square root of x
sin(x) sine of x
asin(x) inverse sine of x
cos(x) cosine of x
acos(x) inverse cosine of x
tan(x) tangent of x
atan(x) inverse tan of x
exp(x) exponential of x
sinh(x) hyperbolic sine of x
cosh(x) hyperbolic cosine of x
tanh(x) hyperbolic tangent of x
ln(x) natural log of x
log(x) log (base 10) of x
rad(x) convert x to radians
deg(x) convert x to degrees
erf(x) error function of x
erfc(x) 1-error function
max(x,y) maximum of x and y
min(x,y) minimum of x and y
sinc(x) sin(x)/x
atan2(x,y) inverse tan (mod 2pi) x = sin, y = cos
sign(x) sign of x (-1,0,1)
mod(x,y) gives remainder of x/y
int(x) truncates to integer
nint(x) nearest integer
ranu(x,y) generates uniform noise between x and y
rang(x,y) generates Gaussian noise with mean x and dispersion y
ranp(x) generates Poisson noise with mean x
ifeq(x,y,a,b) returns a if x equal y, else b
ifne(x,y,a,b) returns a if x not equal y, else b
ifgt(x,y,a,b) returns a if x greater y, else b
ifge(x,y,a,b) returns a if x greater or equal y, else b
iflt(x,y,a,b) returns a if x less y, else b
ifle(x,y,a,b) returns a if x less or equal y, else b
Special functions have been implemented that can retrieve data from data sets (e.g. give the value of the central pixel in an image) or can get information from GIPSY descriptors (i.e. headers containing FITS keywords), ASCII files or GIPSY tables.
: use the whole file; n:m use line numbers n to m; :n use line numbers 1 to n; n: use line numbers n to the end of the file; n use only line number n.Examples:
Expressions are evaluated whenever the task requests the parameter from Hermes. E.g., a parameter which is defined as the expression 'ranu(0,1)' causes a different value to be sent to the task each time it is requested. Likewise a parameter which refers to an image function will have a different value when the underlying image has changed since the last request.
Logicals are decoded in the following way: YES, JA and TRUE result in a logical which is true; NO, NEE and FALSE give a logical which is false. It is sufficient to give the first letter of the possible affirmative and negative replies. Any other answer will be rejected as an error.
Examples:PLOTGRIDS=N OK=YES
Normally character strings are case-sensitive, but individual tasks can deviate from this or convert to either uppercase or lowercase. Some programs require an array of strings. The strings should then be separated by blanks or commas. Sometimes spaces however can be part of the string. Then the input is called 'text'.
Examples:INSTRUME=WSRT (character string) COMMENT=Set smoothed on 2-2-92 (text)
Image data in GIPSY is stored in so called sets. A set consists of two components: an image component and a descriptor component. These components are stored in separate files, but in GIPSY they are always used together.
The image data is stored in a 'crystalline' structure with a virtually unlimited (up to 20) number of dimensions. Image data is only referenced using coordinates on symbolic axes. File coordinates are hidden from the user.
Within a set subsets (or slices) can be defined. A subset is a part of a set with a dimensionality not greater than the dimensionality of the set. So in a three-dimensional set ('cube') the following subset types can be identified:
Associated with the image data there exists a hierarchical system of descriptor (or 'header') items. Headers can be associated with any of all possible subsets, ranging from the whole data set down to the pixel level.
Many tasks operate only on a part of a subset. Such a part is called a frame.
A typical GIPSY set with radio data might be a 3-dimensional 'cube' named AURORA, with axes RA, DEC and FREQ. Pixel, or grid, coordinates in this set can be seen as tuples: (RA,DEC,FREQ). This set AURORA is used as an example in some of the next sections.
When a task requires a set or subset specification, it depends on the operations defined in that program, what subset types are allowed. A subset can be specified by giving the axis name(s) and grids for each subset. For instance,
AURORA
specifies the whole 3-dimensional 'cube';
AURORA FREQ 3
specifies the subset FREQ=3 (i.e. the RA-DEC 'plane' at FREQ grid 3)
of the set AURORA.
Similarly,
AURORA FREQ 1 2 3 4 8
(or: AURORA FREQ 1:4 8)
specifies 5 subsets: 5 RA-DEC planes in AURORA;
AURORA DEC 5:10 FREQ 10
specifies 1-dimensional subsets ('lines') for values of DEC from 5 through 10
at FREQ 10.
Specifying only the axis name, and no grids, selects all subsets
along that axis:
AURORA FREQ
selects all RA-DEC planes in AURORA.
And finally the extreme example 'AURORA RA DEC FREQ' specifies as many subsets as there are pixels in the set AURORA.
Many tasks require one or more positions in a (sub)set. Positions can for instance be used:
The most common position is a grid position in a map, e.g.:
POS= 3 5
It is also possible to enter a number in the physical
units corresponding to a subset axis. Then the number should be followed by valid
units, e.g.
POS= 1418.6 MHz
which is equivalent to:
POS= 1.4186 GHz
Physical units that GIPSY recognizes are given in the table below.
DEGREE ARCSEC ARCMIN RADIAN
CIRCLE DMSSEC DMSMIN DMSDEG
HMSSEC HMSMIN HMSHOUR
METER ANGSTROM NM MICRON
MM CM INCH FOOT
YARD M KM MILE
PC KPC MPC
TICK SECOND MINUTE HOUR
DAY YEAR
HZ KHZ MHZ GHZ
M/S MM/S CM/S KM/S
K MK
JY MJY
TAU
For spatial positions (images with a sky system) more formats are possible.
For example in the AURORA FREQ 10 subset, RA and DEC can be specified
as follows:
POS=* 14 26 9 * -12 3 5.4
For n-dimensional subsets an n-tuple coordinate must be specified.
For instance POS=3 5 10 specifies the same grid point as
above but now for the 'unsliced' 3-dimensional set AURORA.
There are two symbols that denote a special spatial position:
COORDS POS=U 2.8125 U 35.70
If the corresponding CUNITs are in degrees, then this position is processed as degrees.
When specifying spatial coordinates, the following prefixes can be used:
* for RA or DEC in resp. HMS and DMS in EPOCH of set *1950 for RA or DEC in resp. HMS and DMS in EPOCH 1950.0 *xxxx.x for RA or DEC in resp. HMS and DMS in EPOCH xxxx.x G Galactic longitude or latitude in degrees E Ecliptic longitude or latitude in degrees S Supergalactic longitude or latitude in degreesExamples:
Many tasks operate on specified parts of (sub)sets. Examples of subsets for which this can be useful are:
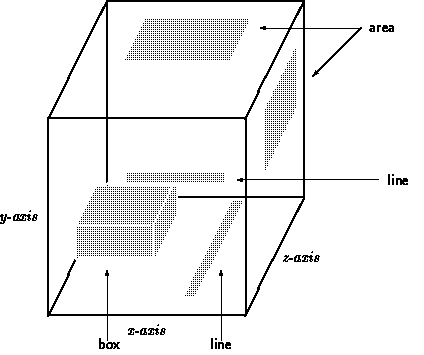
Similar to the POS= keyword, the BOX= keyword is accompanied by a message for the user indicating along which axes he or she needs to specify the limits:
Give BOX in RA,DEC: [entire subset]
BOX=
A box is specified with two positions. For example in a 2-dimensional image we need one for the lower left, and one for the upper right corner of the frame. These positions can be specified in the same formats as used for the POS= keyword (see above). For example,
BOX= -3 -3 4 4
specifies a 2-dimensional box containing 64 pixels.
Boxes can also be specified using a position-and-size notation:
center D size
e.g.
BOX= PC D 8 8
(The D stands for Delta.)
If only the size is given, the user will be prompted to supply the center
position.
BOX= * 3 0 0 * 45 0 0 D 6 arcmin 6 arcmin
to get a box centered at 3h0m0s and 45d0m0s with sizes in RA and Dec of
6 minutes of arc. The units of the sizes must be compatible with the
axis units in the header of the set.
or:
BOX= G 56.7 G 9.89 D 12 ARCSEC 10 ARCSEC
This is the input for a box centered at 56.7° galactic longitude and
9.89° latitude with size 12×10 seconds of arc.
February 21, 2007